Восстановление нелинейной функции нейронной сетью с активацией¶

Нейронная сеть с нелинейностью: теория¶

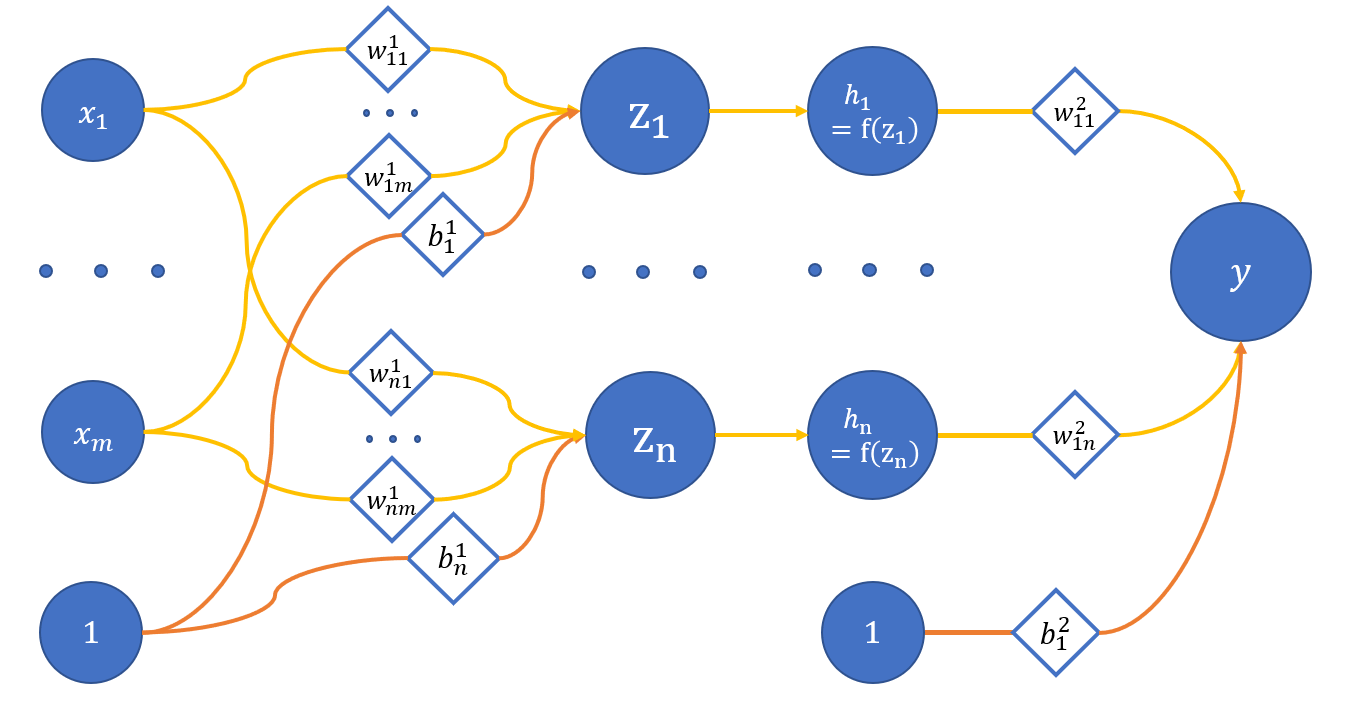
Как мы показали в прошлом туториале, восстановить нелинейную функцию нейронной сетью, не содержащей нелинейность, невозможно. Для того, чтобы это исправить, вспомним об активации нейронов, о которой говорилось в Восстановлении линейной функции одним нейроном:

Рисунок 1. Схема сети с одним скрытым слоем и активацией

где

$x_1 .. x_m$ - вход сети;

$z_1 .. z_n$ - нейроны скрытого слоя;

$h_1 .. h_n$ - активации с помощью функции $f$ соответствующих нейронов скрытого слоя;

$y$ - выход сети;

$w_{ij}^{(l)}$ - веса соответствующих связей между нейронами;

$l$ - номер слоя, $i$ - нейрон на $l + 1$ слое, $j$ - нейрон на $l$ слое;

$b_i^{(l)}$ - смещения на соответствующих слоях.

Возьмём сеть из предыдущего туториала, где было три входа и три нейрона на скрытом слое. Тогда единственное отличие - это наличие активации после скрытого слоя:

$y = \sum_{j=1}^{n} w_{1j}^{(2)}h_j + b_1^{(2)} = W^{(2)}h + b^{(2)} = w_{11}^{(2)}h_1 + w_{12}^{(2)}h_2 + w_{13}^{(2)}h_3 + b_{1}^{(2)}$

где $h_j = f(z_j)$ .

Соответственно изменится и вычисление градиента для параметра

$\begin{equation} \frac{\partial{J}}{\partial{w_{11}^{(1)}}} = \frac{\partial{J}}{\partial{y}} \frac{\partial{y}}{\partial{h_1}} \frac{\partial{h_1}}{\partial{z_1}} \frac{\partial{z_1}}{\partial{w_{11}^{(1)}}} \end{equation}$

В качестве функции активации возьмём ReLU, для которой:

$\begin{equation} \begin{matrix} \ f'(x) & = & \left\{ \begin{matrix} 0, & \mbox{если } x < 0 \\ 1, & \mbox{если } x \geq 0 \end{matrix} \right. \end{matrix} \end{equation}$

Нейронная сеть с нелинейностью: код¶

Начало скрипта:

import numpy as np
import matplotlib.pyplot as plt


def show(x, y, pred=None, title=None):
    plt.plot(x, y, linewidth=5, color="black", antialiased=True, label="True values")

    if pred is not None:
        plt.plot(x, pred, linewidth=2, color="orange", antialiased=True, label="Predicted values")
    if title is not None:
        plt.title(f'{title}')
    plt.legend()
    plt.show()


def showSubplots(x, y, *args, title=None):
    fig = plt.figure(1, figsize=[10.4, 4.8])

    for i, arg in enumerate(args):
        i += 1
        ax = fig.add_subplot(int("12{}".format(i)))

        ax.plot(x, y, linewidth=5, color="black", antialiased=True, label="True values")

        yp = arg["y"]
        name = arg["name"]
        color = arg["color"]

        ax.plot(x, yp, linewidth=2, color=color, antialiased=True, label="{}".format(name))

        ax.legend()
    if title is not None:
        fig.suptitle(f'{title}')
    fig.show()

Возьмём классы Linear и Net из туториала Восстановлении линейной функции нейронной сетью:

class Linear:
    def __init__(self, insize, outsize, name=None):
        self.w = np.random.randn(insize, outsize)
        self.b = np.zeros((outsize, ))

        self.inData = None
        self.data = None

        self.grad = None

        self.name = name


    def __call__(self, data):
        return self.forward(data)


    def forward(self, data):
        self.inData = data
        self.data = np.dot(data, self.w) + self.b

        return self.data


    def backward(self, grad):
        delta = np.dot(grad, self.w.T)
        self.grad = grad

        return delta


    def update(self, lr=0.1):
        self.w -= np.dot(self.inData.T, self.grad) * lr
        self.b -= np.dot(self.grad.T, np.ones(self.grad.shape[0], )) * lr

class Error:
    @staticmethod
    def value(true, pred):
        return 0.5 * np.mean((true - pred) ** 2)


    @staticmethod
    def grad(true, pred):
        c = 1 / np.prod(true.shape)
        return -(true - pred) * c

class Net:
    def __init__(self):
        self.layers = []


    def __call__(self, data):
        return self.predict(data)


    def __getitem__(self, item):
        return self.layers[item]


    def append(self, layer):
        self.layers.append(layer)


    def backward(self, grad):
        for layer in self.layers[::-1]:
            grad = layer.backward(grad)


    def update(self, lr):
        for layer in self.layers:
            layer.update(lr)


    def predict(self, data):
        for layer in self.layers:
            data = layer.forward(data)

        return data


    def optimize(self, data, target, lr):
        prediction = self(data)

        #print("Simple net error {}".format(Error.value(target, prediction)))

        grad = Error.grad(target, prediction)

        self.backward(grad)
        self.update(lr)

X = np.linspace(-3, 3, 1024, dtype=np.float32).reshape(-1, 1)

def func(x):
    from math import sin
    return 2 * sin(x) + 5

f = np.vectorize(func)
Y = f(X)

Добавляется новый класс - Activation, реализующий ReLU активацию:

class Activation:
    def __init__(self, name="relu"):
        self.name = name

        self.inData = None
        self.data = None

        self.grad = None


    def forward(self, data):
        self.inData = data

        self.data = data * (data > 0)

        return self.data


    def backward(self, grad):
        self.grad = (self.data > 0) * grad

        return self.grad


    def update(self, lr):
        pass

Обучение сети¶

Для случая нелинейной функции мы вводим новый трюк - перемешивание данных. Раньше мы формировали батч из значений, идущих подряд друг за другом, теперь же в батче могут встречаться точки из разных концов области определения функции:

def trainNet(size, steps=1000, batchsize=10, learnRate=1e-2):
    np.random.seed(1234)

    net = Net()
    net.append(Linear(insize=1, outsize=size, name="layer_1"))
    net.append(Activation(name="act_layer"))
    net.append(Linear(insize=size, outsize=1, name="layer_2"))

    predictedBT = net(X)

    XC = X.copy()
    perm = np.random.permutation(XC.shape[0])
    XC = XC[perm, :]

    for i in range(steps):
        idx = np.random.randint(0, 1000 - batchsize)
        x = XC[idx:idx + batchsize]
        y = f(x).astype(np.float32)

        net.optimize(x, y, learnRate)

    predictedAT = net(X)

    showSubplots(
        X,
        Y,
        {
            "y": predictedBT,
            "name": "Net results before training",
            "color": "orange"
        },
        {
            "y": predictedAT,
            "name": "Net results after training",
            "color": "orange"
        }
    )

trainNet(5, steps=1000, batchsize=100)

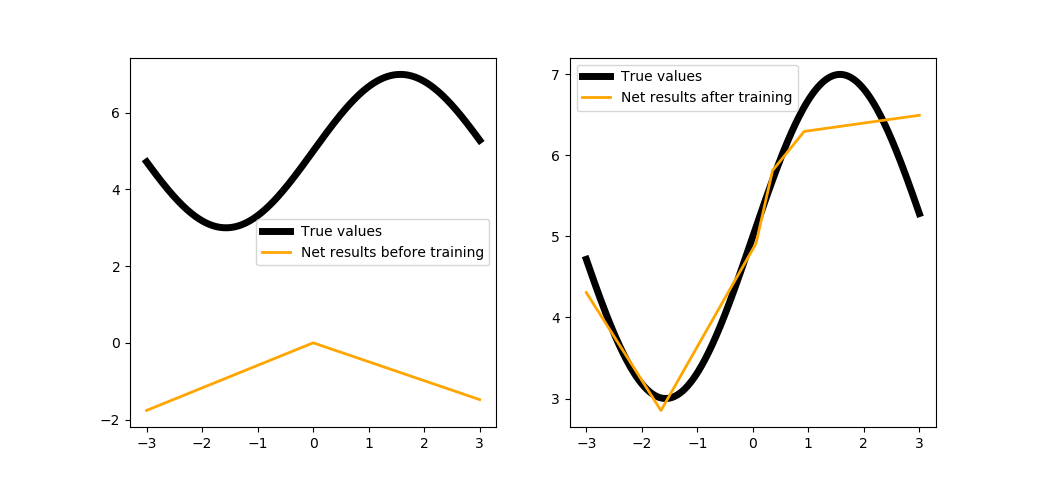
Рисунок 2. Сравнение результатов сети (5 нейронов в скрытом слое) до и после обучения

Как видите, сеть стремится описать нашу функцию, причём каждый нейрон в скрытом слое отвечает за свой участок кривой. Логично было бы попробовать увеличить количество нейронов:

trainNet(100, steps=1000, batchsize=100)

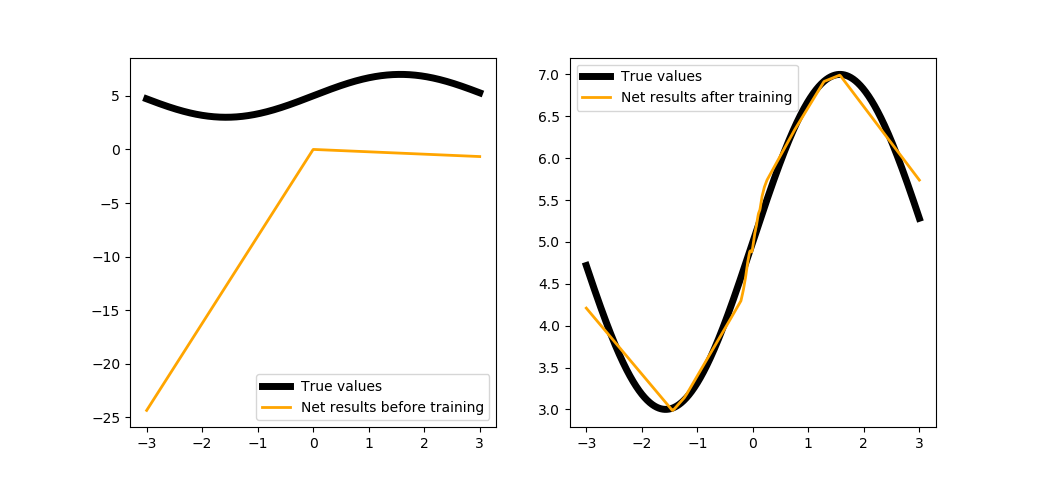
Рисунок 3. Сравнение результатов сети (100 нейронов в скрытом слое) до и после обучения

Уже лучше, но всё равно есть погрешность. У нас есть возможность увеличить количество шагов, чтобы повысить качество, но это будет долго, так что самое время воспользоваться более мощными инструментами библиотеки PuzzleLib.

Реализация инструментами библиотеки¶

Заметьте, что в этот раз мы обучаем сеть не по шагам (прогон одного батча), а по эпохам (прогон всей выборки), и ещё выбираем более продвинутый оптимизатор:

def trainNetPL(size, epochs, batchsize=10, learnRate=1e-2):
    from PuzzleLib.Modules import Linear, Activation
    from PuzzleLib.Modules.Activation import relu
    from PuzzleLib.Containers import Sequential
    from PuzzleLib.Optimizers import MomentumSGD
    from PuzzleLib.Cost import MSE
    from PuzzleLib.Handlers import Trainer
    from PuzzleLib.Backend.gpuarray import to_gpu

    np.random.seed(1234)

    net = Sequential()
    net.append(Linear(insize=1, outsize=size, initscheme="gaussian"))
    net.append(Activation(activation=relu))
    net.append(Linear(insize=size, outsize=1, initscheme="gaussian"))

    predictedBT = net(to_gpu(X)).get()

    cost = MSE()
    optimizer = MomentumSGD(learnRate)
    optimizer.setupOn(net)

    trainer = Trainer(net, cost, optimizer, batchsize=batchsize)

    show(X, Y, net(to_gpu(X)).get())

    XC, YC = X.copy(), Y.copy()
    perm = np.random.permutation(XC.shape[0])
    XC = XC[perm, :]
    YC = YC[perm, :]

    for i in range(epochs):
        trainer.trainFromHost(XC.astype(np.float32), YC.astype(np.float32), macroBatchSize=1000,
                                onMacroBatchFinish=lambda train: print("PL module error: %s" % train.cost.getMeanError()))

    net.evalMode()

    predictedAT = net(to_gpu(X)).get()

    showSubplots(
        X,
        Y,
        {
            "y": predictedBT,
            "name": "PL net results before training",
            "color": "orange"
        },
        {
            "y": predictedAT,
            "name": "PL net results after training",
            "color": "orange"
        }
    )

trainNetPL(100, epochs=100, batchsize=100)

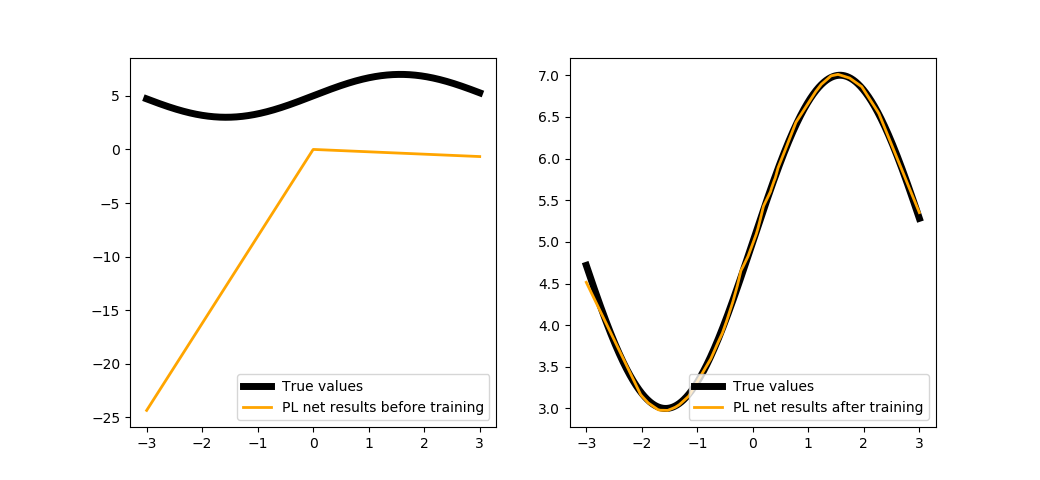
Рисунок 4. Сравнение результатов сети PL до и после обучения

Заключение¶

В общем и целом можно сказать, что любые фреймворки для глубокого обучения - это, в первую очередь, библиотеки для автоматического дифференцирования вычислительных графов, и никакой магии тут нет. Надеемся, мы помогли читателю избавиться от неуверенности из-за пробелов в понимании работы нейронных сетей, так что, может быть, вы даже поучаствуете в развитии библиотеки PuzzleLib, написав свой собственный модуль.