Восстановление линейной функции одним нейроном

Запустить в Google Colab

Посмотреть на GitHub

Скачать ноутбук

Искусственный нейрон

В прошлой статье говорилось о модели, имеющей набор параметров $\theta$, который нам необходимо оптимизировать, чтобы минимизировать функцию ошибки $J(\theta)$. Когда речь идёт о глубоком обучении, под такими моделями понимают сами искусственные нейронные сети, которые состоят из узлов - нейронов.

Математически искусственный нейрон обычно представляют как некоторую нелинейную функцию от единственного аргумента — линейной комбинации всех входных сигналов - сигнал от которой посылается на единственный выход. На рисунке 1 наглядно представлена схема искусственного нейрона:

Рисунок 1. Схема искусственного нейрона

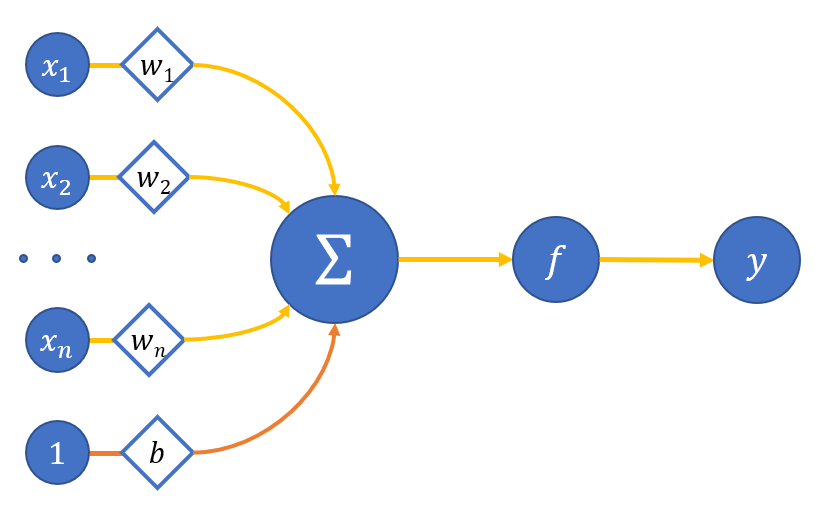
где

$x_0,...,x_n$ - входы нейрона;

$w_o,..w_n$ - веса соответствующих входов;

$b$ - вес смещения (принимаем вход этой связи равным единице);

$\sum$ - сумматор взвешенных входов;

$f$ - функция активации нейрона;

$y$ - выход нейрона.

В итоге получается, что выход нейрона выглядит так:

$$y = f(\sum_{i=1}^{n} x_iw_i + b)$$

или если обозначить вес смещения как $w_0$, а значение входа $x_0$:

$$y = f(\sum_{i=0}^{n} x_iw_i)$$

Функция активации может быть, например, такой, что она будет давать на выходе 1, если линейная комбинация всех нейронов превышает какое-то значение, и 0 в обратном случае.

Если в качестве модели, о которой говорилось выше, мы возьмём один такой нейрон, то его веса и будут теми самыми параметрами модели $\theta$.

Давайте для простоты рассмотрим модель упрощённого нейрона с одним входом и без функции активации (пока что) - рисунок 2:

Рисунок 2. Схема упрощённого нейрона

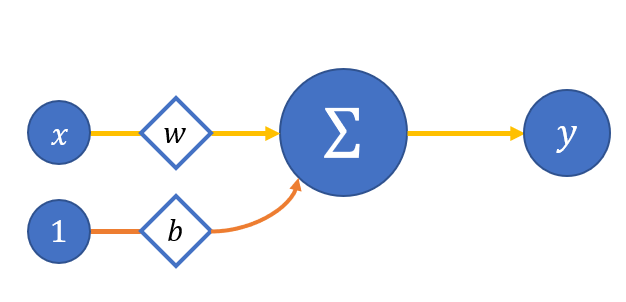
Тогда:

$$y = xw + b$$

что подозрительно напоминает уравнение прямой. Так давайте её и будем восстанавливать.

Для этого, как говорилось, необходимо решить оптимизационную задачу:

$$\sum_{i=0}^{l} J(\theta) \to \min\limits_{\theta}$$

Возьмём в качестве функции ошибки среднеквадратичную (двойка в знаменателе добавляется для удобства последующего дифференцирования):

$$J(\theta) = \frac{1}{2N}\sum_{i=1}^N(y_i-y_i^p)^2 = \frac{1}{2N}\sum_{i=1}^N(y_i-(x_iw + b))^2$$

где

$N$ - количество объектов в выборке;
$y_i$ - реальное значение для i-го объекта;
$y_i^p$ - предсказанное моделью значение для i-го объекта.

Вспомним, как оптимизируются параметры:

$$\theta_{t+1} = \theta_t - \eta \cdot \frac{1}{l}\sum_{i=0}^{l} \nabla_{\theta}{J_i(\theta_t)}$$

или для случая с упрощённым нейроном:

$$\begin{equation} w_{t+1} = w_t - \eta \cdot \frac{1}{l}\sum_{i=0}^{l} \nabla_{w}{J_i(w_t, b_t)} \end{equation}$$

$$\begin{equation} b_{t+1} = b_t - \eta \cdot \frac{1}{l}\sum_{i=0}^{l} \nabla_{b}{J_i(w_t, b_t)} \end{equation}$$

Как найти $\nabla_{w}{J_i(w_t, b_t)}$ и $\nabla_{w}{J_i(w_t, b_t)}$? Необходимо просто взять частные производные функции ошибки от этих параметров, которые, в свою очередь, будут производными сложной функции:

$$\begin{equation} \frac{\partial{J}}{\partial{w}} = \frac{\partial{J}}{\partial{y}}\frac{\partial{y}}{\partial{w}} \end{equation}$$

$$\begin{equation} \frac{\partial{J}}{\partial{b}} = \frac{\partial{J}}{\partial{y}}\frac{\partial{y}}{\partial{b}} \end{equation}$$

Для выбранной функции ошибки имеем следующие аналитические выражения:

$$\begin{equation} \frac{\partial{J}}{\partial{y}} = -(y-y^p) \end{equation}$$

$$\begin{equation} \frac{\partial{y}}{\partial{w}} = x \end{equation}$$

$$\begin{equation} \frac{\partial{y}}{\partial{b}} = 1 \end{equation}$$

Тогда обновление параметров искусственного нейрона происходит следующим образом:

$$\begin{equation} w_{t+1} = w_t - \eta \cdot \frac{1}{l}\sum_{i=0}^{l} (-(y_i-y_i^p) \cdot x_i) \end{equation}$$

$$\begin{equation} b_{t+1} = b_t - \eta \cdot \frac{1}{l}\sum_{i=0}^{l} (-(y_i-y_i^p)) \end{equation}$$

Ну что же, пора всё это воплотить в коде.

Упрощённый нейрон в коде

Для начала импортируем всё, что нам понадобится - это numpy для работы с тензорами, matplotlib.pyplot для построения графиков и напишем функции show и showSubplots для отображения графиков на экране:

import numpy as np
import matplotlib.pyplot as plt


def show(x, y, pred=None, title=None):
    plt.plot(x, y, linewidth=5, color="black", antialiased=True, label="True values")

    if pred is not None:
        plt.plot(x, pred, linewidth=2, color="orange", antialiased=True, label="Predicted values")
    if title is not None:
        plt.title(f'{title}')
    plt.legend()
    plt.show()


def showSubplots(x, y, *args, title=None):
    fig = plt.figure(1, figsize=[10.4, 4.8])

    for i, arg in enumerate(args):
        i += 1
        ax = fig.add_subplot(int("12{}".format(i)))

        ax.plot(x, y, linewidth=5, color="black", antialiased=True, label="True values")

        yp = arg["y"]
        name = arg["name"]
        color = arg["color"]

        ax.plot(x, yp, linewidth=2, color=color, antialiased=True, label="{}".format(name))

        ax.legend()
    if title is not None:
        fig.suptitle(f'{title}')
    fig.show()

Далее зададим множество аргументов нашей линейной функции и саму эту функцию:

X = np.linspace(-3, 3, 1000, dtype=np.float32).reshape(-1, 1)

def func(x):
    return 2 * x + 3

f = np.vectorize(func)
Y = f(X)

show(X, Y)

Рисунок 3. Линейная функция

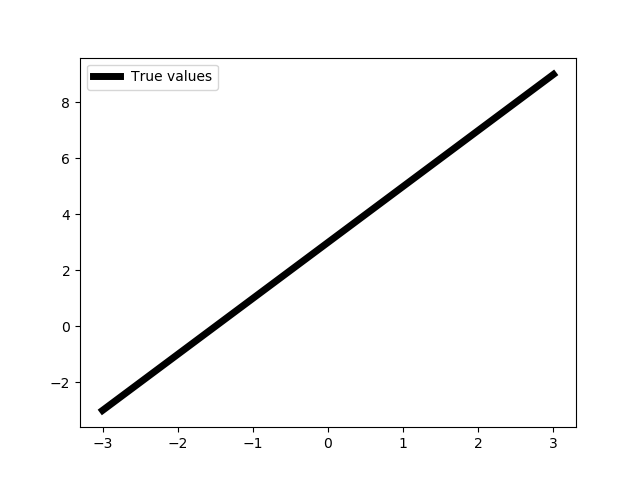
Тип данных np.float32 не обязателен для нас сейчас, но понадобится в будущем.

Создадим простенькую реализацию выбранной функции ошибки - среднеквадратичной ошибки:

class Error:
    @staticmethod
    def value(true, pred):
        return 0.5 * np.mean((true - pred) ** 2)


    @staticmethod
    def grad(true, pred):
        c = 1 / np.prod(true.shape)
        return -(true - pred) * c

c - коэффициент среднего, обратный количеству объектов в выборке.

Наконец сам класс искусственного нейрона:

class Neuron:
    def __init__(self):
        self.w = 1
        self.b = 0

        self.inData = None
        self.data = None

        self.grad = None


    def __call__(self, data):
        return self.forward(data)


    def forward(self, data):
        self.inData = data
        self.data = data * self.w + self.b

        return self.data


    def backward(self, grad):
        self.grad = grad


    def update(self, lr=0.1):
        self.w -= self.inData * self.grad * lr
        self.b -= self.grad * lr


    def optimize(self, data, target, lr):
        prediction = self(data)

    #   print("Neuron error {}".format(Error.value(target, prediction)))

        grad = Error.grad(target, prediction)

        self.backward(grad)
        self.update(lr)

Объясним методы:

• forward - прямой прогон данных через нейрон; нам необходимо здесь запоминать в атрибутах класса входящие данные, потому что они понадобятся при оптимизации параметров (см. $x$ в формуле обновления весов выше);
• backward - задел на будущее, пока что просто сохраняем пришедший градиент от функции ошибки в атрибутах класса;
• update - обновление параметров нейрона по вышеприведённой формуле;
• optimize - метод, объединяющий в себе все необходимые операции для оптимизации параметров нейрона; lr - learning rate.

Можно переходить к обучению нейрона.

Обучение нейрона

Инициализируем нейрон и покажем, какие значения по сравнению с искомой функцией он выдаёт. В данном примере обучение происходит не по батчу и не по всей выборке, а по каждому отдельно взятому объекту этой выборки:

def trainNeuron(steps=200, learnRate=1e-2):
    neuron = Neuron()

    predictedBT = [neuron(x) for x in X]

    for i in range(steps):
        idx = np.random.randint(0, 1000)
        x = X[idx]
        y = f(x).astype(np.float32)

        neuron.optimize(x, y, learnRate)

    predictedAT = [neuron(x) for x in X]

    showSubplots(
        X,
        Y,
        {
            "y": predictedBT,
            "name": "Net results before training",
            "color": "orange"
        },
        {
            "y": predictedAT,
            "name": "Net results after training",
            "color": "orange"
        }
    )

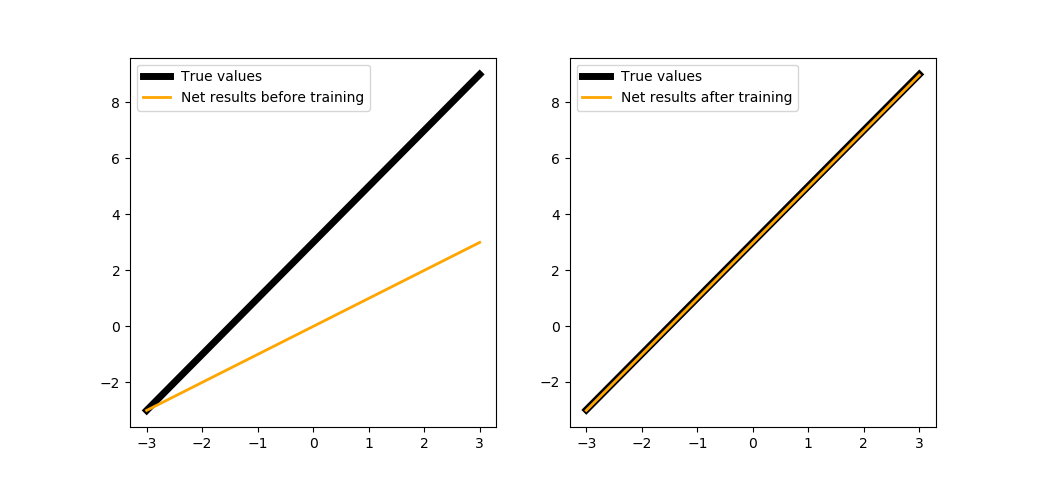
При запуске на 200 шагах:

trainNeuron(200)

Рисунок 4. Сравнение результатов нейрона до и после обучения на 200 шагах

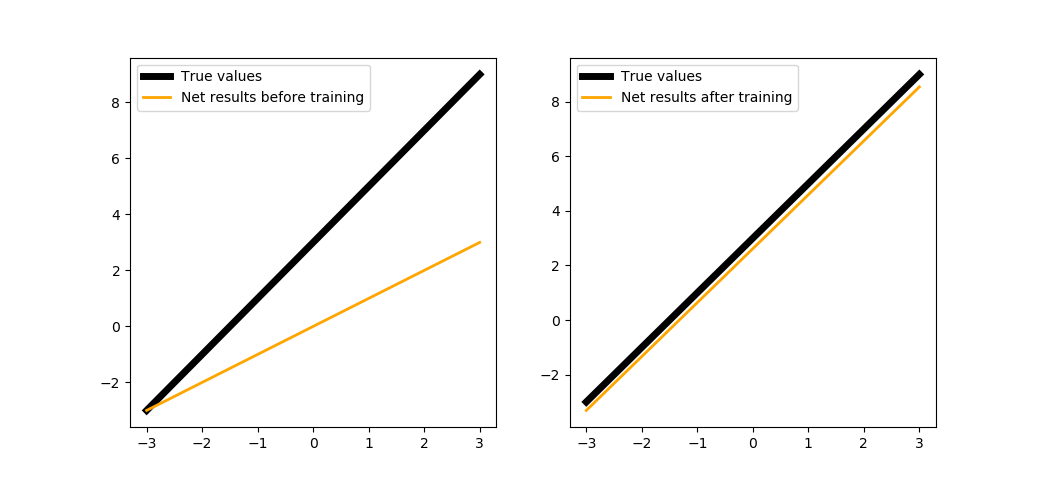
Можем обучить нейрон чуть подольше:

trainNeuron(500)

Рисунок 5. Сравнение результатов нейрона до и после обучения на 500 шагах

Следующий раздел покажет, как это реализовано в PuzzleLib.

Реализация инструментами библиотеки

Заведём отдельную функцию, в которой обучение нашего самописного нейрона будет проходить параллельно с нейроном, сделанным инструментами библиотеки.

Для работы обучения нейрона на PuzzleLib нам понадобятся модуль линейного слоя, через который будем имитировать нейрон, оптимизатор, функцию ошибки и функцию для размещения тензоров на выбранном устройстве (как правило, GPU) to_gpu:

def trainBoth(steps=1000, learnRate=1e-2):
    from PuzzleLib.Modules import Linear
    from PuzzleLib.Optimizers import SGD
    from PuzzleLib.Cost import MSE
    from PuzzleLib.Backend.gpuarray import to_gpu

Далее объявим функцию, которая будет проводить оптимизацию нашего псевдонейрона:

    def optimizeModule(module, cost, optimizer, data, target):
        module.trainMode()

        data = to_gpu(data.reshape(-1, 1))
        target = to_gpu(target.reshape(-1, 1))

        error, grad = cost(module(data), target)
        print("PL module error {}".format(error))

        module.zeroGradParams()
        module.backward(grad, updGrad=False)
        optimizer.update()

Решейп данных необходим, так как PuzzleLib предъявляет определённые требования к размерности входных данных.

Создадим псевдонейрон и заполним значения весов и смещений так, чтобы они совпадали с нашим самописным нейроном:

    neuronPL = Linear(insize=1, outsize=1)
    neuronPL.W.fill(1)
    neuronPL.b.fill(0)

Далее инициализируем функцию ошибки и оптимизатор, а также устанавливаем последний на псевдонейрон:

    cost = MSE()
    optimizer = SGD(learnRate)
    optimizer.setupOn(neuronPL)

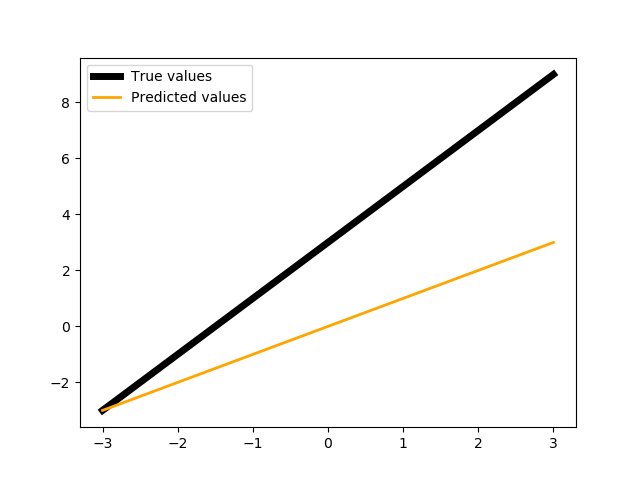
Покажем значения псевдонейрона:

    show(X, Y, neuronPL(to_gpu(X)).get())

И наконец обучим оба нейрона:

    for i in range(steps):
        idx = np.random.randint(0, 1000)
        x = X[idx]
        y = f(x).astype(np.float32)

        perceptron.optimize(x, y, learnRate)

        cost.resetAccumulator()
        optimizeModule(neuronPL, cost, optimizer, x, y)

    neuronPL.evalMode()

    showSubplots(
            X,
            Y,
            {
                "y": [perceptron(x) for x in X],
                "name": "Neuron",
                "color": "orange"
            },
            {
                "y": neuronPL(to_gpu(X)).get(),
                "name": "PuzzleLib neuron",
                "color": "magenta"
            }
    )

trainBoth(500)

Рисунок 6. Сравнение значений искомой функции и необученного псевдонейрона

Рисунок 7. Сравнение значений обученных нейронов

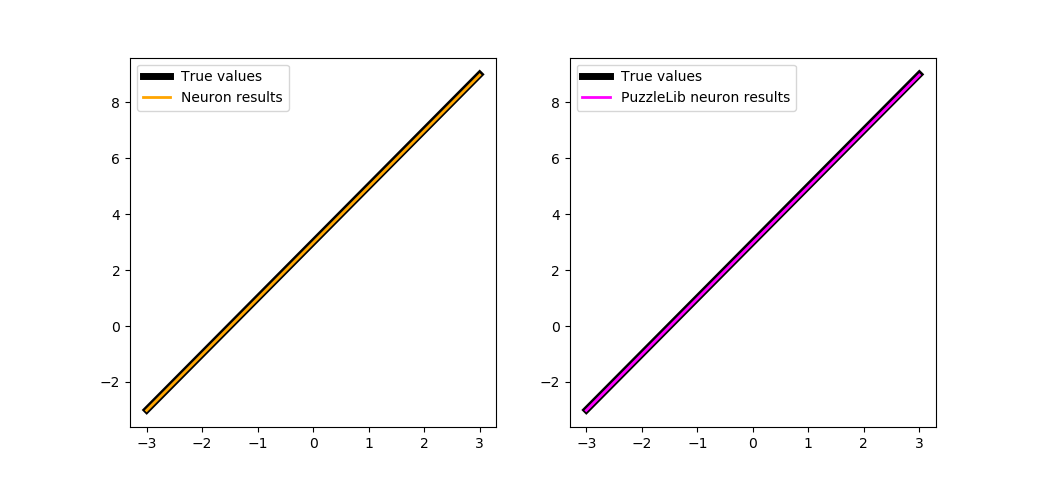
Стоит также отметить, что в библиотеке предусмотрены обработчики, которые снимают с нас необходимость вручную создавать функции подобные optimizeModule, причём в них уже предусмотрено обучение по батчам. Если переписать функцию trainBoth с использованием обработчика, то получится так:

def trainBoth(steps=1000, learnRate=1e-2):
    from PuzzleLib.Modules import Linear
    from PuzzleLib.Optimizers import SGD
    from PuzzleLib.Cost import MSE
    from PuzzleLib.Handlers import Trainer
    from PuzzleLib.Backend.gpuarray import to_gpu

    neuronPL = Linear(insize=1, outsize=1)
    neuronPL.W.fill(1)
    neuronPL.b.fill(0)

    cost = MSE()
    optimizer = SGD(learnRate)
    optimizer.setupOn(neuronPL)

    trainer = Trainer(neuronPL, cost, optimizer, batchsize=1)

    perceptron = Neuron()

    show(X, Y, neuronPL(to_gpu(X)).get())

    for i in range(steps):
        idx = np.random.randint(0, 1000)
        x = X[idx]
        y = f(x).astype(np.float32)

        perceptron.optimize(x, y, learnRate)

        trainer.trainFromHost(x.reshape(-1, 1), y.reshape(-1, 1), macroBatchSize=1,
                                onMacroBatchFinish=lambda train: print("PL module error: %s" % train.cost.getMeanError()))

    neuronPL.evalMode()

    showSubplots(
        X,
        Y,
        {
            "y": [perceptron(x) for x in X],
            "name": "Neuron",
            "color": "orange"
        },
        {
            "y": neuronPL(to_gpu(X)).get(),
            "name": "PuzzleLib neuron",
            "color": "magenta"
        }
    )

Дополнительно: Роль смещения в нейроне

Интересно посмотреть - что будет, если убрать у нейрона параметр смещения? Перепишем методы нейрона так, чтобы исключить смещение при прямом проходе данных:

    def forward(self, data):
        self.inData = data
        self.data = data * self.w

        return self.data

trainNeuron(500)

Рисунок 8. Сравнение результатов нейрона без смещения до и после обучения

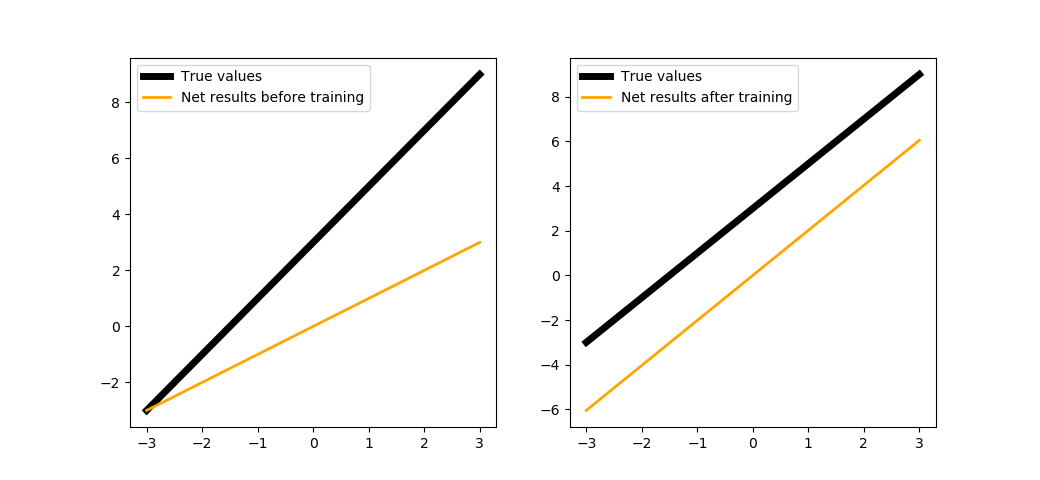
Как видите, нейрон без смещения смог выстроиться параллельно искомой функции, но для полного её восстановления ему не хватило того самого смещения.