InstanceNorm2D

Описание

Info

Родительский класс: Module

Производные классы: -

Этот модуль реализует операцию двумерной индивидуальной нормализации.

Индивидуальная нормализация применяется для обучения генеративных нейронных сетей, для которых нормализация по батчу оказывает негативное влияние и на скорость обучения, и на качество результата. В батч-нормализации статистики вычисляются по нескольким изображениям, из-за чего информация о каждом отдельном изображении теряется.

Рисунок 1. Демонстрация принципов действия различных видов нормализации

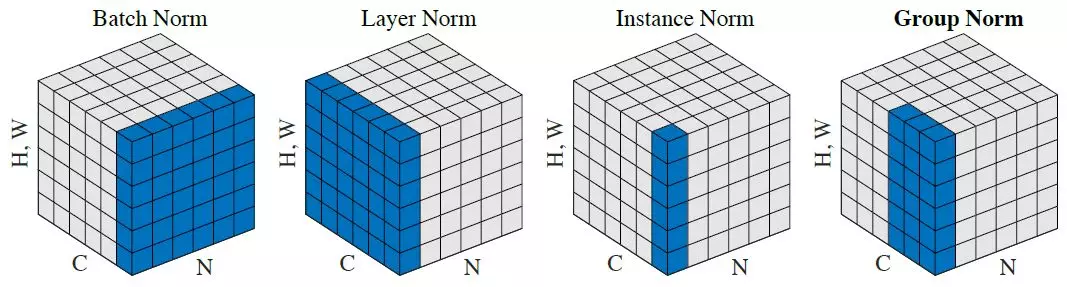
Тензор данных на входе в модуль имеет размерность $(N, C, H, W)$, где $N$ - размер батча, $C$ - количество карт (каналов), $H$ - высота карты, $W$ - ширина карты. Условимся насчёт индексов: $t$ - номер элемента батча, $i$ - номер карты, $m$ - номер элемента карты признаков по высоте, $n$ - номер элемента карты признаков по ширине. Тогда для каждой отдельно взятой комбинации $t$-го элемента батча и $i$-ой карты признаков:

$$\begin{equation} \mu_{ti} = \frac{1}{HW}\sum_{m=1}^{H} \sum_{m=1}^{W}x_{timn} \end{equation}$$

$$\begin{equation} \sigma_{ti}^2 = \frac{1}{HW}\sum_{m=1}^{H} \sum_{m=1}^{W}(x_{timn} - \mu_{ti})^2 \end{equation}$$

$$\begin{equation} \hat{x}_{timn} = \frac{x_{timn} - \mu_{ti}}{\sqrt{\sigma_{ti}^2 + \epsilon}} \end{equation}$$

$$\begin{equation} y_{timn} = \gamma\hat{x}_{timn} + \beta \end{equation}$$

где

$\mu_{ti}$ - математическое ожидание распределения признаков для отдельно взятой комбинации $t$-го элемента батча и $i$-ой карты признаков;
$\sigma_{ti}^2$ - дисперсия распределения признаков для отдельно взятой комбинации $t$-го элемента батча и $i$-ой карты признаков;
$x_{timn}$ - элемент карты признаков;
$\hat{x}_{timn}$ - нормализованный элемент карты признаков;
$\epsilon$ - стабилизирующая константа, предотвращающая деление на ноль;
$\gamma$ - аффинный параметр масштаб;
$\beta$ - аффинный параметр сдвиг.

На практике, ограничение в лице нулевого мат ожидания и единичной дисперсии может сильно ограничить предсказательную способность сети, поэтому добавляются ещё два обучаемых аффинных параметра: масштаб и сдвиг, чтобы алгоритм мог подстроить под себя значения среднего и дисперсии.

Дополнительные источники

• Подробнее про выбор типа нормализации: github
• Подробнее про индивидуальную нормализацию: arxiv

Инициализация

def __init__(self, numOfMaps, epsilon=1e-5, affine=True, name=None):

Параметры

Параметр	Возможные типы	Описание	По умолчанию
numOfMaps	int	Количество карт	-
epsilon	float	Коэффициент малого сдвига	1e-5
affine	bool	Использование аффинных преобразований	True
name	str	Имя слоя	None

Пояснения

affine - флаг, который отвечает за то, будут ли scale и bias (масштаб и сдвиг) параметры слоя батч-нормализации обучаемыми, либо они будут зафиксированы (1 и 0 соответственно), в следствие чего слой будет проводить только операцию нормализации по среднему и дисперсии.

Примеры

Необходимые импорты.

import numpy as np
from PuzzleLib.Backend import gpuarray
from PuzzleLib.Modules import InstanceNorm2D

Info

gpuarray необходим для правильного размещения тензора на GPU

batchsize, maps, h, w = 5, 3, 4, 4
data = gpuarray.to_gpu(np.random.randn(batchsize, maps, h, w).astype(np.float32))
instNorm2d = InstanceNorm2D(numOfMaps=maps)
instNorm2d(data)