MomentumSGD

Описание

Info

Родительский класс: SGD

Производные классы: -

Данный модуль реализует принцип работы стохастического градиентного спуска с моментом (momentum stochastic gradient descent - MomentumSGD).

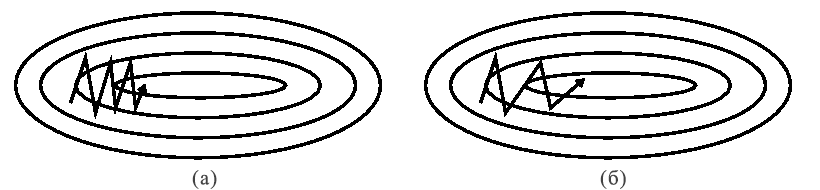
Обычный стохастический градиентный спуск имеет ряд недостатков, один из которых - это трудности работы с "оврагами" функции ошибки - теми участками поверхности, на которых имеется ощутимый разброс скорости изменения функции в зависимости от направления (см. рисунок 1.а). В таких случаях алгоритм SGD тратит большую часть энергии на осцилляцию вдоль склонов "оврага", из-за чего продвижение к минимуму затормаживается.

Применение дополнительного момента в этом алгоритме позволяет притушить колебания и ускорить продвижение в релевантном направлении (см. рисунок 1.б).

Рисунок 1. (а) Обычный SGD, (б) SGD с моментом

Аналитически это выражается добавлением коэффициента сохранения $\gamma$, который отвечает за то, какую часть градиента с предыдущего шага учитывать при подсчёте на текущем шаге (здесь мы в целях упрощения опускаем некоторые обозначения, которые присутствовали в формулах для SGD):

\begin{equation} g_t = \gamma{g_{t-1}} + (1 - \gamma)\eta\nabla_\theta J(\theta_t) \end{equation} \begin{equation} \theta_{t+1} = \theta_t - g_t \end{equation}

где

$\theta_{t+1}$ - обновлённый набор параметров для следующего шага оптимизации;
$\theta_t$ - набор параметров на текущем шаге;
$\gamma$ - коэффициент сохранения (обычно берётся порядка 0.9);
$\eta$ - скорость обучения (в некоторых вариантах формулы множитель $(1 - \gamma)$ включён в неё);
$\nabla_{\theta}J(\theta_t)$ - градиент функции ошибки.

Инициализация

def __init__(self, learnRate=1e-3, momRate=0.9, nodeinfo=None):

Параметры

Параметр	Возможные типы	Описание	По умолчанию
learnRate	float	Скорость обучения	1e-3
momRate	float	Коэффициент сохранения	0.9
nodeinfo	NodeInfo	Объект, содержащий информацию о вычислительном узле	None

Пояснения

-

Примеры

---

Необходимые импорты:

import numpy as np
from PuzzleLib.Optimizers import MomentumSGD
from PuzzleLib.Backend import gpuarray

Info

gpuarray необходим для правильного размещения тензора на GPU.

Создадим синтетическую обучающую выборку:

data = gpuarray.to_gpu(np.random.randn(16, 128).astype(np.float32))
target = gpuarray.to_gpu(np.random.randn(16, 1).astype(np.float32))

Объявляем оптимизатор:

optimizer = MomentumSGD(learnRate=0.01, momRate=0.85)

Пусть уже есть некоторая сеть net, определённая, например, через Graph, тогда, чтобы установить оптимизатор на сеть, требуется следующее:

optimizer.setupOn(net, useGlobalState=True)

Info

Подробнее про методы оптимизаторов и их параметры читайте в описании родительского класса Optimizer

Также пусть есть некая функция ошибки loss, наследованная от Cost, рассчитывающая в т.ч. её градиент. Тогда получаем реализацию процесса оптимизации:

for i in range(100):
... predictions = net(data)
... error, grad = loss(predictions, target)

... optimizer.zeroGradParams()
... net.backward(grad)
... optimizer.update()

... if (i + 1) % 5 == 0:
...   print("Iteration #%d error: %s" % (i + 1, error))