DeconvND

Description

Info

Parent class: Module

Derived classes: Deconv1D, Deconv2D, Deconv3D

General information

This module performs the operation of n-dimensional transposed convolution (inverse convolution, fractionally-strided convolution). The name "deconvolution", although established, is not an exact description of the operation.

When a convolution operation is performed (see ConvND) over a data tensor, a certain amount of information is irretrievably lost, which makes it possible to construct several versions of operations that perform a roughly opposite action. The transposed convolution operation is one of them.

Let us presume there is a map $I_{4x4}$:

$$I = \begin{pmatrix} a_1 & a_2 & a_3 & a_4 \\ b_1 & b_2 & b_3 & b_4 \\ c_1 & c_2 & c_3 & c_4 \\ d_1 & d_2 & d_3 & d_4 \\ \end{pmatrix}$$

As well as the convolution kernel $W_{3x3}$:

$$W = \begin{pmatrix} w_{00} & w_{01} & w_{02} \\ w_{10} & w_{11} & w_{12} \\ w_{20} & w_{21} & w_{22} \\ \end{pmatrix}$$

Then we can represent the convolution kernel as a convolution matrix: $C_{4x16}$:

$$C = \begin{pmatrix} w_{00} & w_{01} & w_{02} & 0 & w_{10} & w_{11} & w_{12} & 0 & w_{20} & w_{21} & w_{22} & 0 & 0 & 0 & 0 & 0 \\ 0 & w_{00} & w_{01} & w_{02} & 0 &w_{10} & w_{11} & w_{12} & 0 & w_{20} & w_{21} & w_{22} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & w_{00} & w_{01} & w_{02} & 0 & w_{10} & w_{11} & w_{12} & 0 & w_{20} & w_{21} & w_{22} & 0 \\ 0 & 0 & 0 & 0 & 0 & w_{00} & w_{01} & w_{02} & 0 & w_{10} & w_{11} & w_{12} & 0 & w_{20} & w_{21} & w_{22} \\ \end{pmatrix}$$

If we multiply this matrix by a flattened map $\text{vec}(I)$: $$ \text{vec}(I) = \begin{pmatrix} a_1 & a_2 & a_3 & a_4 & b_1 & b_2 & b_3 & b_4 & c_1 & c_2 & c_3 & c_4 & d_1 & d_2 & d_3 & d_4 \ \end{pmatrix}^T $$

we will get a flattened output map $\text{vec}(O)$: $$ \text{vec}(O) = \begin{pmatrix} m_1 & m_2 & m_3 & m_4 \ \end{pmatrix}^{T} $$

which is then converted to a full output map $O_{2x2}$:

$$ O = \begin{pmatrix} m_1 & m_2 \ m_3 & m_4 \ \end{pmatrix} $$ $\hat{I}_{4x4}$ But, as one can see, another operation is also possible: we can restore the $\hat{I}_{4x4}$ map from the $O_{2x2}$ map through multiplying $\text{vec}(O)$ by the transposed convolution matrix:

$$\text{vec}(\hat{I}) = C^T\text{vec}(O)$$

Hence the name of this operation: transposed convolution.

Unlike the Upsample module, this module is trainable, therefore, significant loss of information in the recoverable elements can be avoided.

Operation Parameters

The following parameters and objects characterize the convolution operation:

---

Convolution kernel size size

---

If you look at the above example, the convolution kernel is the tensor $W^T$. The convolution kernel is characterized by its size, shape and a set of values of its elements. For convolution layers of a neural network, a set of values of the kernel elements is represented by the weights that are a trained parameter.

Important

Within this library, the shape of convolution kernels is always equilateral, i.e. a square for two-dimensional convolution and a cube for three-dimensional one.

---

Convolution stride stride

---

Within the transposed convolution operation, the stride parameter means the stride of the direct convolution, the use of which would lead to the given O tensor. For more information on this parameter for a direct convolution, please see ConvND.

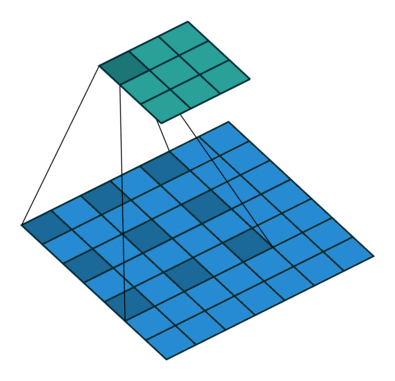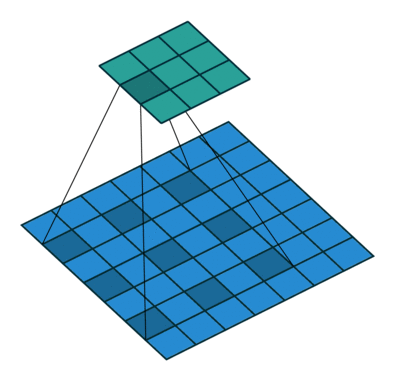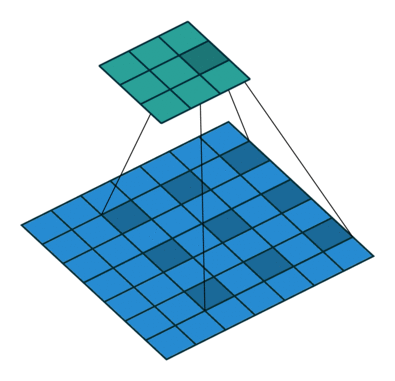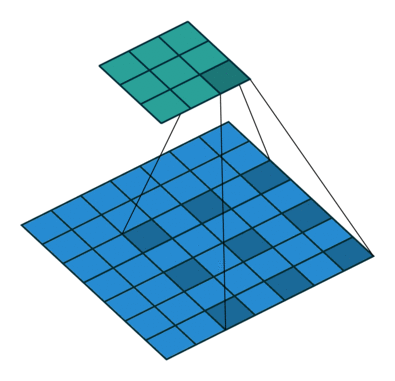
Let us take a two-dimensional convolution with a kernel of size 3 and a stride of 2 (Figure 1):

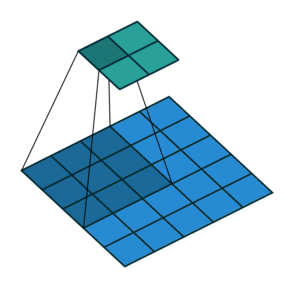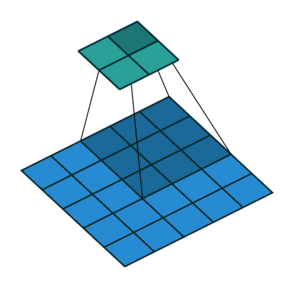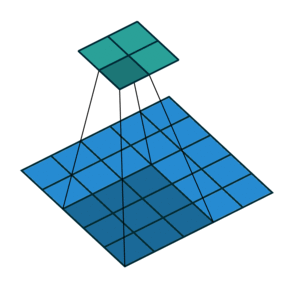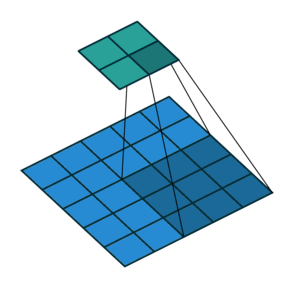
Figure 1. Two-dimensional convolution (size = 3, stride = 2)

To perform the deconvolution restoring the original 5x5 map, we will need to “divide” its stride by adding zero elements between the tensor elements obtained after the direct convolution, hence the second name of this operation is fractionally-strided convolution:

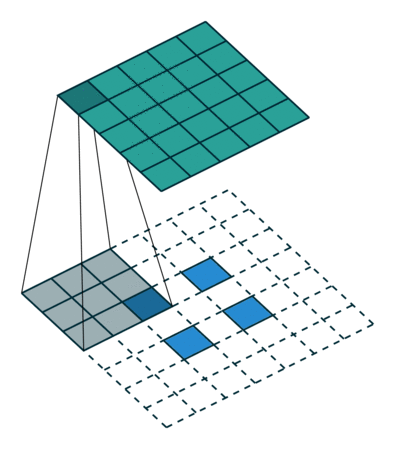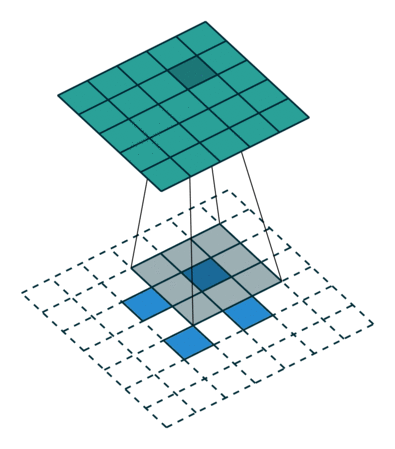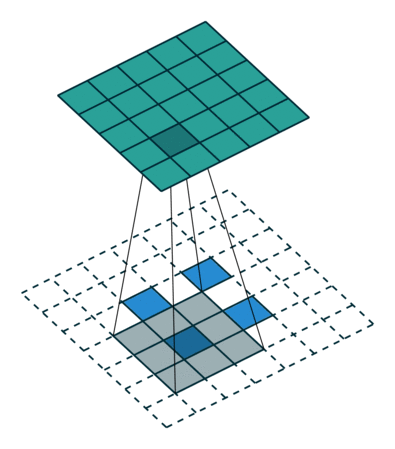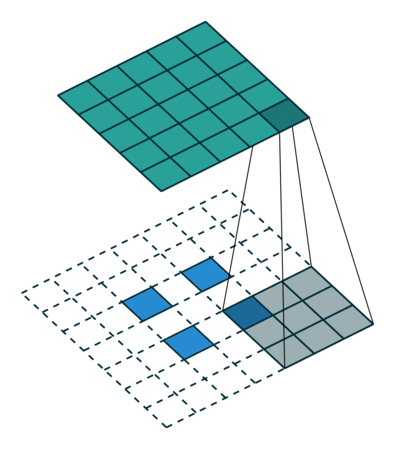
Figure 2. Two-dimensional deconvolution (size = 3, stride = 2)

---

Padding pad

---

Within the transposed convolution operation, the padding parameter means the padding of the initial tensor before the direct convolution, the use of which would lead to the given $O$ tensor. For more information on this parameter for a direct convolution, please see ConvND.

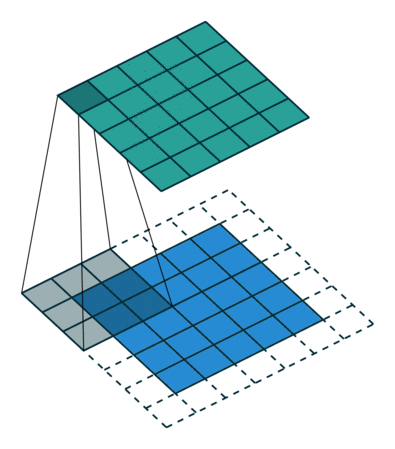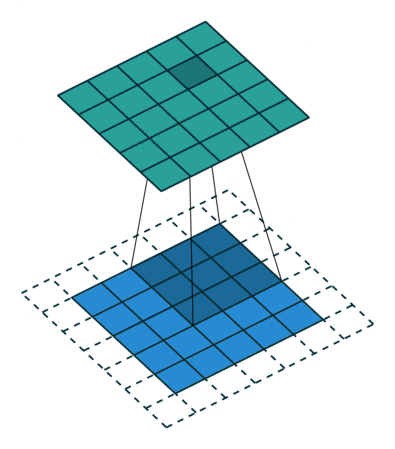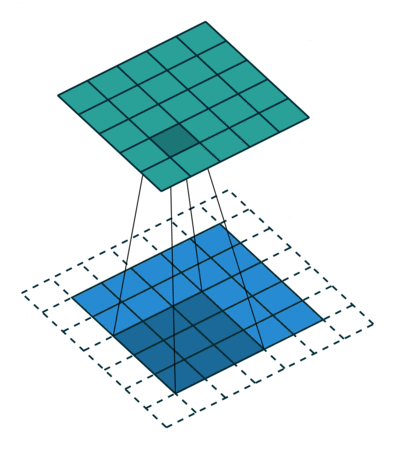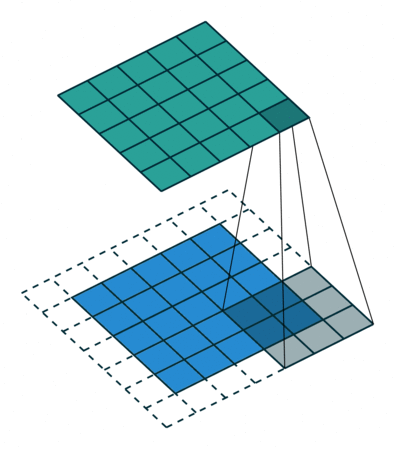
To understand the principle, we need to look at the parallel operation of the direct and inverse convolutions. For example, if pad = 2 is used for a direct convolution with size = 4, stride = 1 parameters on a 5x5 size map, the resulting map will be of 6x6 size (see Figure 3). That is, to perform an inverse convolution (see Figure 4), it is necessary to understand, which parameters of the direct convolution have led to the current tensor.

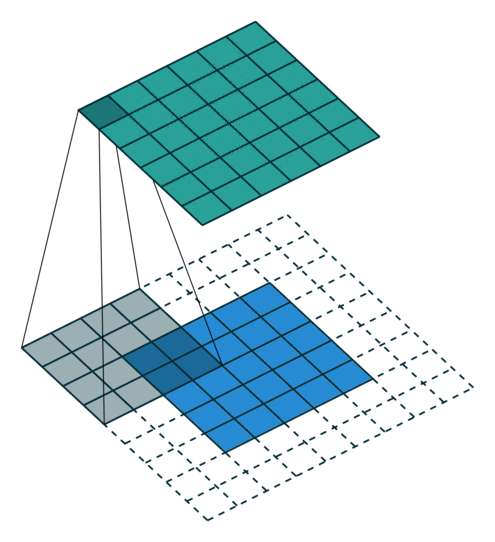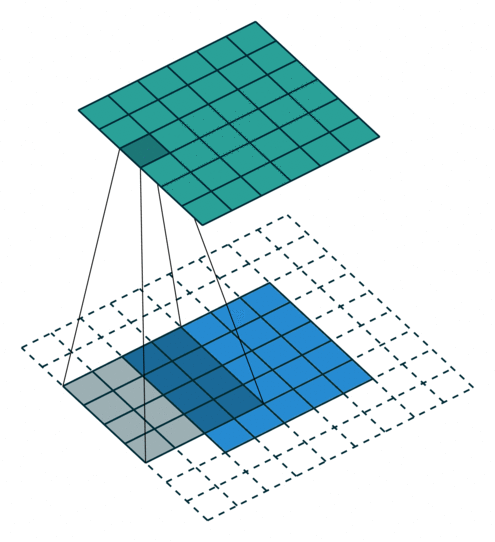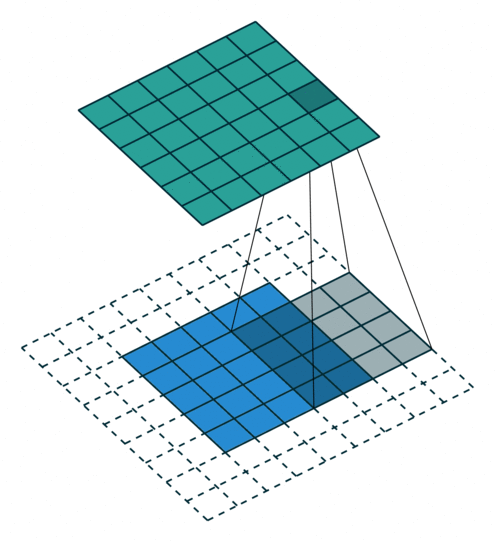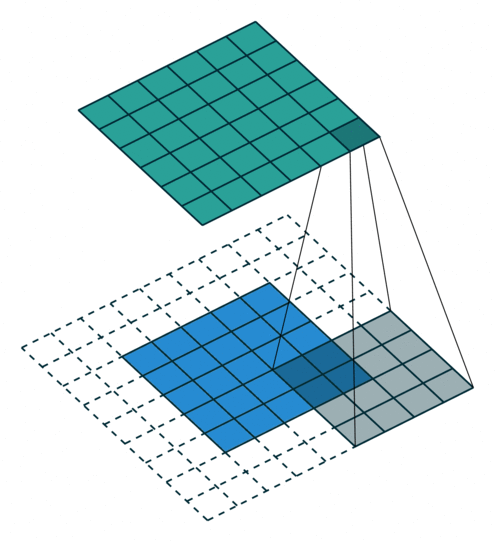
Figure 3. Two-dimensional direct convolution (size = 4, stride = 1, pad = 2)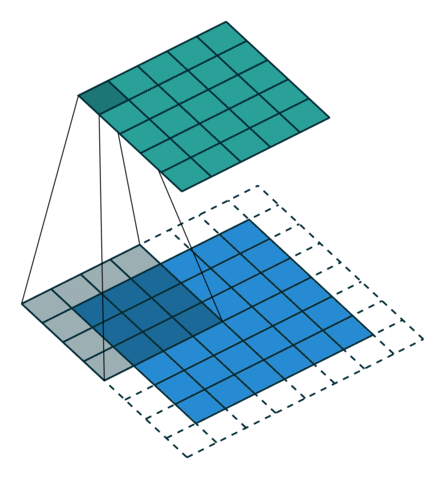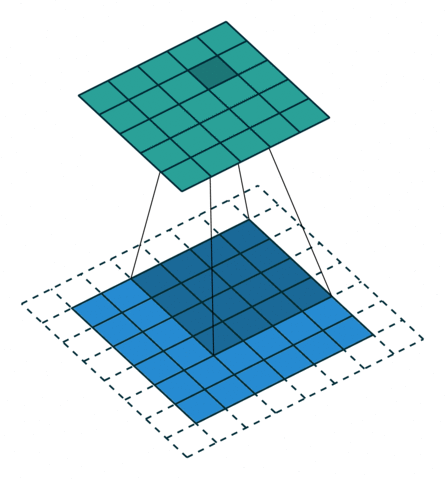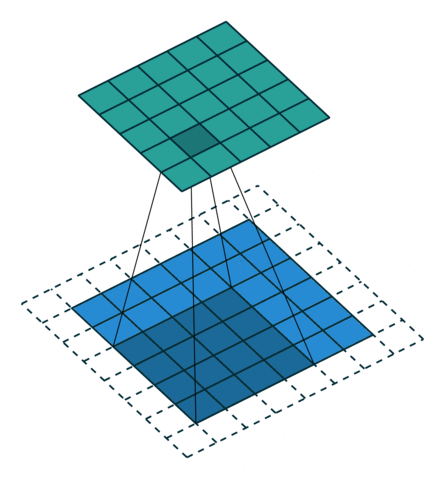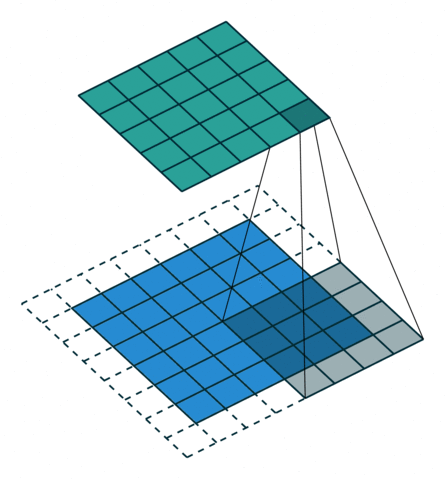

Figure 4. Two-dimensional inverse convolution (size = 4, stride = 1, pad = 2)

If we use the same parameters as those, which preserve the tensor shape in the direct convolution, we can expect to get the identical demonstration of the inverse convolution operation:

Figure 5. Two-dimensional forward and inverse convolution (size = 3, stride = 1, pad = 1)

---

Dilation dilation

---

The dilation parameter determines the number of times by which the size of the convolution kernel will be increased. Therewith, the kernel elements are moved apart by a specified number, while the resulting empty values are filled with zeros.

Figure 6. Dilated convolution of a map of size 7 (size = 3, stride = 1, dilation = 1)

A nice feature of this technique is that it is cheap in terms of computation. That is, we use convolutions of a much larger dimension, increase the sensitivity fields, being able to track more global features - but without burdening the hardware.

---

Number of connections between the input and output maps groups

---

-

Additional sources

• Differences between backward convolution and upsample operations: link;
• Theano Convolution Arithmetic Theory: link;
• Visual demonstration of the transposed convolution: link.

Initializing

def __init__(self, nd, inmaps, outmaps, size, stride=1, pad=0, dilation=1, wscale=1.0, useBias=True, name=None,
                 initscheme=None, empty=False, groups=1):

Parameters

Parameter	Allowed types	Description	Default
nd	int	Dimension of the operation	-
inmaps	int	Number of maps in the input tensor	-
outmaps	int	Number of maps in the output tensor	-
size	int	Convolution kernel size	-
stride	int, tuple	Convolution stride	1
pad	int, tuple	Map padding	0
dilation	int	Convolution window dilation	1
wscale	float	Random layer weights variance	1.0
useBias	bool	Whether to use the bias vector	True
initscheme	Union[tuple, str]	Specifies the layer weights initialization scheme (see createTensorWithScheme)	None -> ("xavier_uniform", "in")
name	str	Layer name	None
empty	bool	Whether to initialize the matrix of weights and biases	False
groups	int	Number of groups the maps are split into for separate processing	1

Explanations

Please see the derived classes.