BatchNormND

Description

Info

Parent class: Module

Derived classes: BatchNorm1D, BatchNorm2D, BatchNorm3D

General information

This module performs the N-dimensional batch normalization operation. The choice of the dimension of the operation depends on the dimension of the input data.

The batch normalization layer is intended, first of all, to solve the problem of covariate shift. The easiest way to understand the covariate shift is with an example: suppose there is a network that must recognize images of cats. The training sample contains images of only black cats, so when we try to process pictures of cats of colors other than black during the tests, the quality of the prediction of the model will be noticeably worse than on a black cat set. In other words, the covariate shift is a situation when the distributions of features in the training and test sets have different parameters (mean, variance, etc.).

When we talk about the covariate shift within the framework of deep learning, in particular, we mean the situation of different distribution of features not at the network input, as in the example above, but in the layers inside the model - the internal covariate shift. A neural network changes its weights with each mini-batch passed (if we use the appropriate optimization mechanism, of course), and since the outputs of the current layer are input features for the next one, each layer in the network gets into a situation where the distribution of input features changes every step, i.e. for every passed mini-batch.

The basic idea of batch normalization is to limit the internal covariate shift by normalizing the output of each layer, transforming them into distributions with zero mean and unit variance.

Figure 1 shows that the batch normalization gets the average and variance for the batch.

Figure 1. Demonstration of the principles of operation of various types of normalization

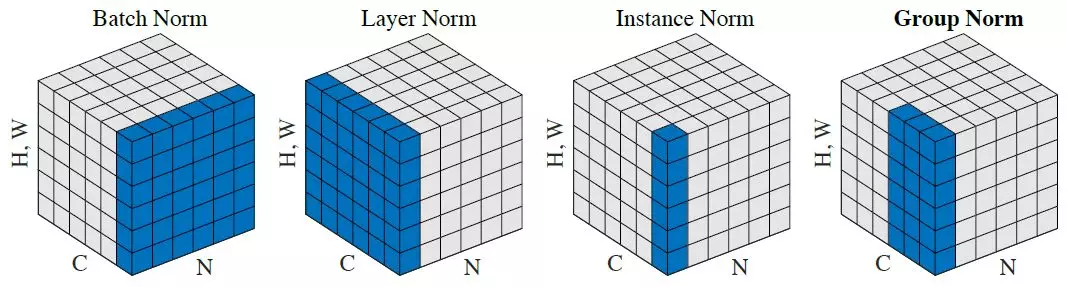
Let us consider the case of batch normalization of two-dimensional maps. Then the data tensor has the shape $(N, C, H, W)$, where $N$ - batch size, $C$ - number of maps (channels), $H$ - height of the map, $W$ - width of the map. Let us agree on the indexes: $t$ - number of the batch element, $i$ - number of the map, $m$ - number of the feature map element in height, $n$ - number of the feature map element in width. Then for each individual $i$-th feature map:

$$\begin{equation} \mu_i = \frac{1}{NHW}\sum_{t=1}^{N} \sum_{m=1}^{H} \sum_{m=1}^{W}x_{timn} \end{equation}$$

$$\begin{equation} \sigma_i^2 = \frac{1}{NHW}\sum_{t=1}^{N} \sum_{m=1}^{H} \sum_{m=1}^{W}(x_{timn} - \mu_i)^2 \end{equation}$$

$$\begin{equation} \hat{x}_{timn} = \frac{x_{timn} - \mu_i}{\sqrt{\sigma_i^2 + \epsilon}} \end{equation}$$

$$\begin{equation} y_{timn} = \gamma\hat{x}_{timn} + \beta \end{equation}$$

where

$\mu_i$ - mean of the distribution of features in the batch for the i-th feature map; $\sigma_i^2$ - mean of the distribution of features in the batch for the i-th feature map; $x_{timn}$ - feature map element;
$\hat{x}_{timn}$ - normalized feature map element;
$\epsilon$ - stabilizing constant, preventing division by zero; $\gamma$ - affine scale parameter;
$\beta$ - affine shift parameter.

For the parameters $\mu_i$ and $\sigma_i^2$ the layers of batch normalization remember the average value over the entire set during training. During inference, these parameters are frozen.

During inference, these parameters are frozen. In practice, the restriction of zero mean and unit variance can greatly limit the predictive ability of the network, so two more trained affine parameters are added: scale and shift, so that the algorithm can adjust the average and variance values for itself.

Additional sources

You can read more about batch normalization in the following sources:

• Link 1;
• Link 2.

Initializing

def __init__(self, nd, maps, epsilon=1e-5, initFactor=1.0, minFactor=0.1, sscale=0.01, affine=True, name=None, empty=False, inplace=False):

Parameters

Parameter	Allowed types	Descripition	Default
nd	int	Dimension of operation	-
size	int	Number of input features	-
epsilon	float	Stabilizing constant	1e-5
initFactor	float	The initial factor value in the moving average	1.0
minFactor	float	The initial factor value in the moving average	0.1
sscale	float	Dispersion of the Gaussian distribution for the scale parameter of batch normalization	0.01
affine	bool	If True, the layer will have trainable affine parameters scale and bias	True
name	str	Layer name	None
empty	bool	If True, the tensors of the parameters of the module will not be initialized	False
inplace	bool	If True, the output tensor will be written in memory in the place of the input tensor	False

Explanations

See derived classes