Pool1D¶
Description¶
General information¶
This module implements an abstract class of one-dimensional pooling.
Pooling is the process of nonlinear compaction of the initial tensor by applying a given mathematical operation (averaging or choosing a maximum value) to the subtensors of the initial tensor. Thus, each element of the output tensor will be the result of the selected operation on the corresponding subtensor.
As a result of applying the pooling operation without using special techniques, the dimension of the maps of the output tensor is smaller than the dimension of the maps of the original one.
For the input tensor of shape (N, C, L_{in}) and the output tensor of shape (N, C, L_{out}) the operation is performed as follows (we consider the i-th element of the batch and the j-th map):
where
N - batch size;
C - number of maps in the tensor;
L - sequence size;
OP - operation of averaging \frac{1}{k}\sum_{m=0}^{k-1} or choosing a maximum value \max\limits_{m=0..k-1};
stride - pooling stride;
k - pooling window size.
The pooling layer often alternates with convolution layers (see ConvND). Pooling, as was mentioned above, conducts nonlinear compaction of feature maps. This implies the following: if during the previous convolution operation a certain set of features was revealed, then a less detailed map is suitable for further processing; the number of calculations will decrease, and the accuracy of the model will not change significantly. Another positive effect of the operation is a decrease in the likelihood of overfitting the model: the model is trained on more abstract representations of objects.
Operation parameters¶
Pooling type
Pooling type implies a mathematical operation that is applied to the current subtensor. Traditionally, these mathematical operations are calculating the average value and calculating the maximum value.
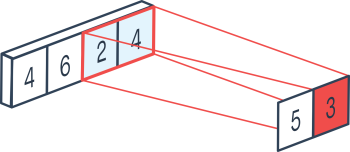
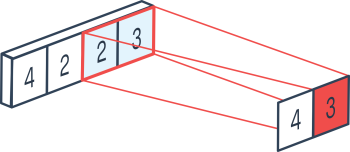
Kernel size size
The size of the pooling kernel is the size of the subtensor that will be the subject of the selected operation.
Pooling stride stride
The pooling stride determines how far the pooling kernel moves each step before interacting with the subset of the map elements. A stride of one means that the kernel slides continuously and does not skip elements. A stride of two means that the kernel skips every other element of the map. This feature helps to reduce the number of calculations and the dimension of the output tensor, working with the same source data.
Padding pad
The padding parameter determines the number of additional layers of elements along the perimeter of the initial input tensor, filled with values according to certain rules. This makes it possible to avoid the loss of boundary elements of maps given the certain sets of other parameters.
The final formula for calculating the size of the output tensor during one-dimensional pooling:
Additional sources¶
Additional links for reference:
Initializing¶
def __init__(self, size=2, stride=2, pad=0, name=None):
Parameters
| Parameter | Allowed types | Description | Default |
|---|---|---|---|
| size | int | Kernel size | 2 |
| stride | int | Pooling stride | 2 |
| pad | int | Pooling stride | 0 |
| name | str | Layer name | None |
Explanations
See derived classes.