ConvND

Description

Info

Parent class: Module

Derived classes: Conv1D, Conv2D, Conv3D

General information

This module performs an n-dimensional convolution.

A convolution in general terms is an operation on a pair of tensors D and B resulting in a tensor $D$ и $B$, resulting in a tensor $C=D∗B$, the tensor $D$ being a subtensor of a certain tensor $A$. Each element of the result is calculated as the scalar product of the tensor $B$ and the subtensor $A$ of the same size (the position of the calculated element in the result depends on the position of $A$).

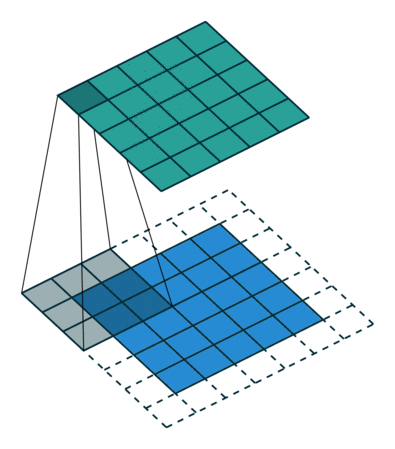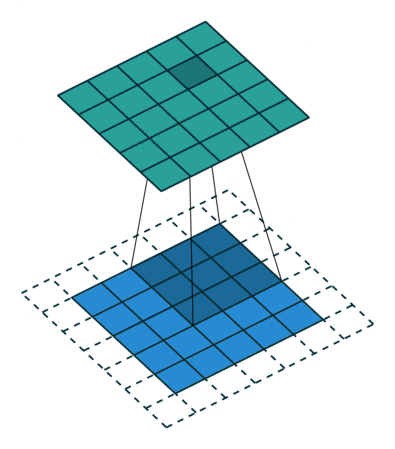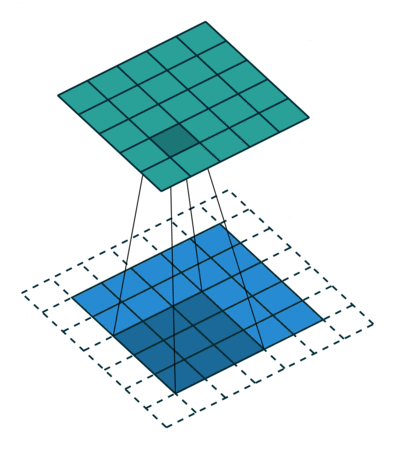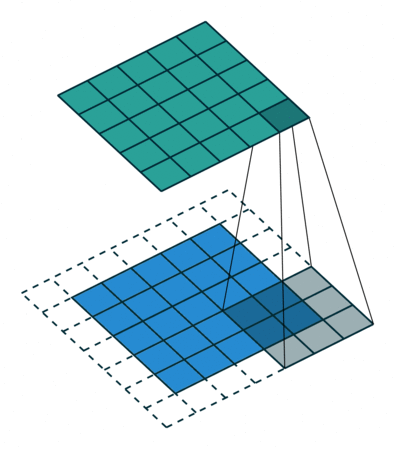
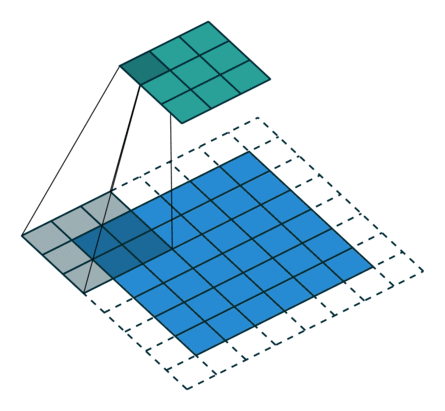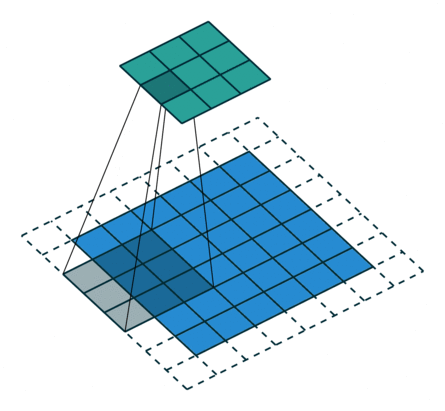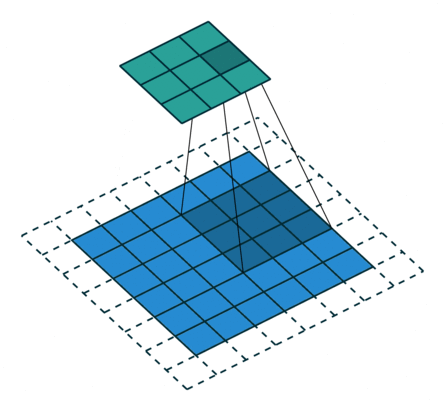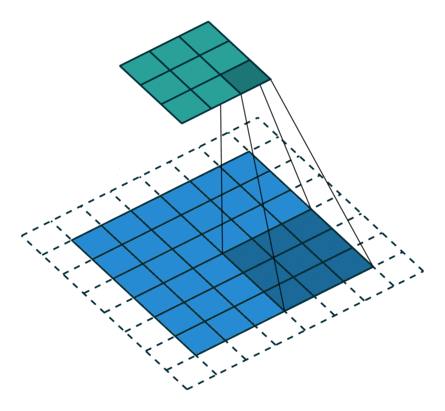
This is best demonstrated in Figure 1 (see the “Convolution Step” parameter).

For an input tensor of shape $(N, C_{in}, Dims_{in})$ and the output of shape $(N, C_{out}, Dims_{out})$ the operation is performed as follows (we consider the i-th element of the batch and the j-th map of the output tensor): $$ out_i(C_{out_j}) = bias(C_{out_j}) + \sum_{k=0}^{C_{in} - 1}weight(C_{out_j}, k) \star input_i(k) $$

where

$N$ - size of the batch;
$C$ - number of maps in the tensor;
$Dims$ - vector of dimensions of the tensor map for each dimension (for example, $(H, W)$ for two-dimensional maps);
$bias$ - tensor of the convolution layer bias;
$weight$ - tensor of the convolution layer weights;
$\star$ - cross correlation operator.

Operation parameters

The following parameters and objects characterize the convolution operation:

---

Convolution kernel size

---

In the definition above, the convolution kernel is the $B$ tensor. The convolution kernel is characterized by its size, shape and set of values of its elements. For the convolutional layers of the neural network, the set of values of the kernel elements is the weights that are a trained parameter.

Important

Within this library, the shape of the convolution kernels is always equilateral, i.e. a square for a two-dimensional convolution and a cube for a three-dimensional one.

---

Convolution stride dstride

---

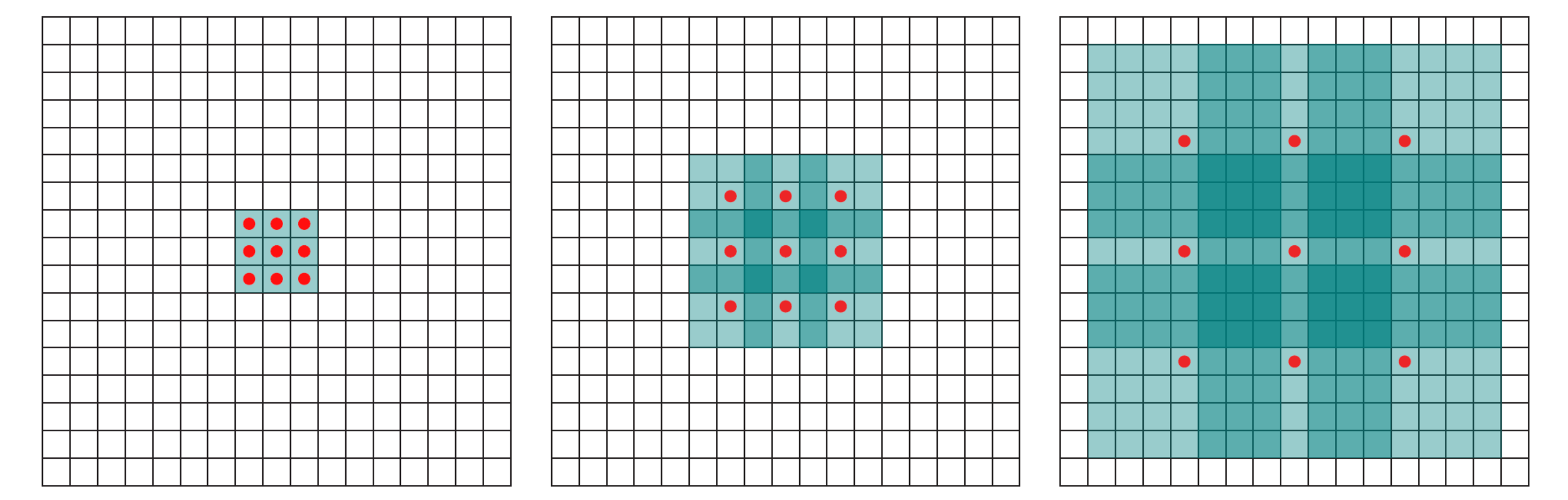
The convolution stride defines how far the convolution kernel moves each step before being multiplied by a subset of the tensor elements. A stride equal to one means that the kernel slides continuously and does not skip elements. A stride of two means that the kernel skips every other element of the tensor. This characteristic helps to reduce the number of calculations and the dimension of the output tensor, working with the same source data.

The operation of the convolution with various stride values is well demonstrated in Figures 1 and 2 (using the example of a two-dimensional convolution):

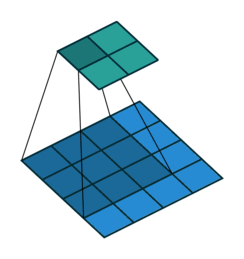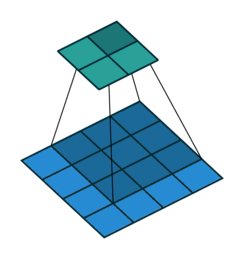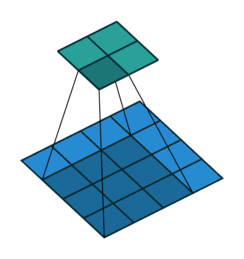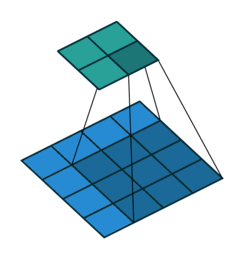
Figure 1. Two-dimensional convolution (size=3, stride=1)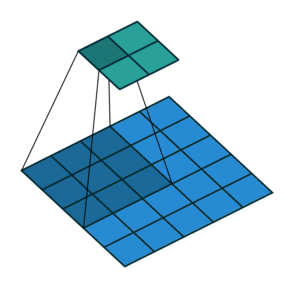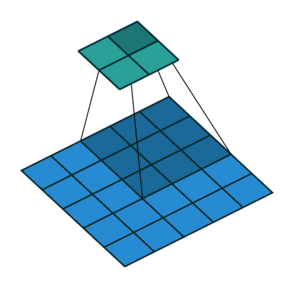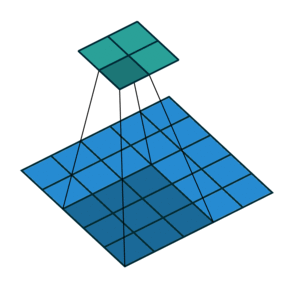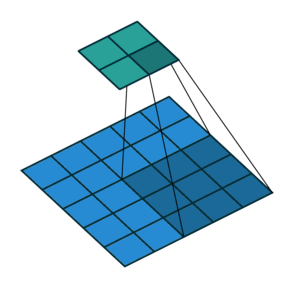

Figure 2. Two-dimensional convolution (size=3, stride=2)

---

Padding pad

---

The padding parameter determines the number of additional layers of elements along the perimeter of the initial input tensor, filled with values according to certain rules. This is necessary, for example, in order to obtain a tensor of the same size as the input one (Figure 3).

Figure 3. Two-dimensional convolution of a size 5 map (size=3, stride=1, pad=1)

Another reason may be the desire to avoid the loss of boundary elements of maps with certain sets of other parameters. Figure 4 shows the situation when the elements were not lost: without padding, the last boundary 2 columns and rows would not be involved in getting the output tensor.

Two-dimensional convolution of a size 6 map (size=3, stride=2, pad=1)

Most often, additional rows of elements are filled with zeros. In addition, other simple filling rules can be set: for example, copying the value of the nearest element.

---

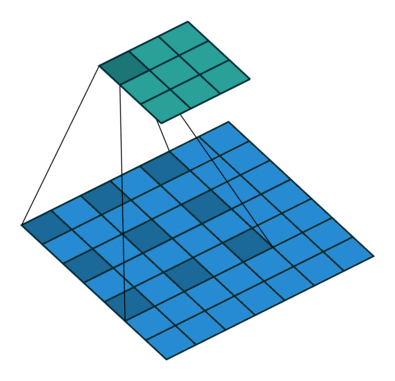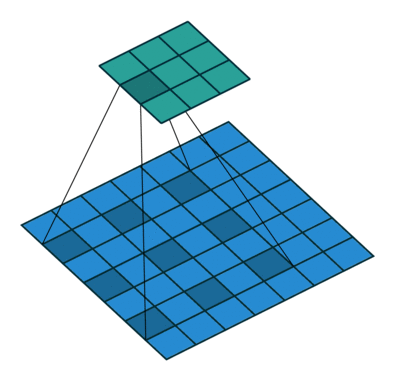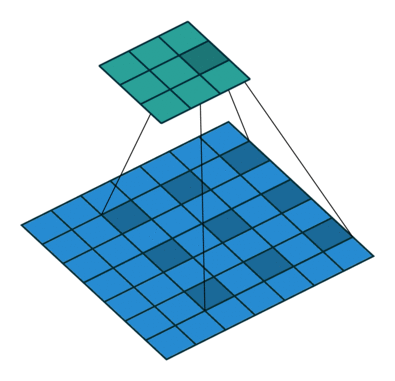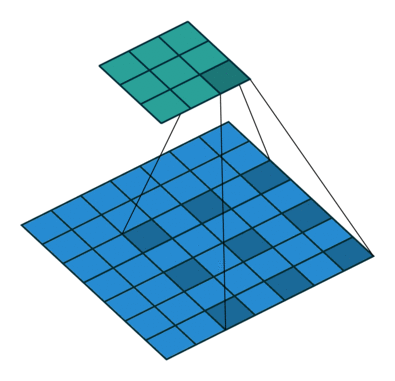
Dilation dilation

---

The dilation parameter determines the number of times by which the size of the convolution kernel will be increased. Therewith, the kernel elements are moved apart by a specified number of times, and the resulting empty values are filled with zeros.

Figure 5. Dilated convolution with different degrees of dilation: dilation = 1, dilation = 2 and dilation = 4

When applied, the dilation exponentially increases the size of the (receptive field). For the first image it is 3x3, for the second it is 7x7, for the third it is 15x15

Another example of a dilated convolution is shown in Figure 6:

Figure 6. Dilated convolution of a size 7 map (size = 3, stride = 1, dilation = 1

A nice feature of this technique is that it is cheap in terms of computation. That is, we use convolutions of a much larger dimension, increase the sensitivity fields, being able to track more global features - but without burdening the hardware.

---

The number of connections between the input and output maps groups

---

The technique of using groups in a convolution operation is called Depthwise Convolution in the English research literature, which is a part of the Depthwise Separable Convolution technique.

Depthwise Separable Convolution breaks down the convolution calculation process into two parts: depthwise convolution and pointwise convolution. Let us consider the technique through the example of a two-dimensional convolution.

At the first stage, the convolution results in a tensor of unchanged depth: we use convolution kernels of depth 1 and size size in an amount equal to the number of input maps, and we apply each such kernel separately to each map respectively.

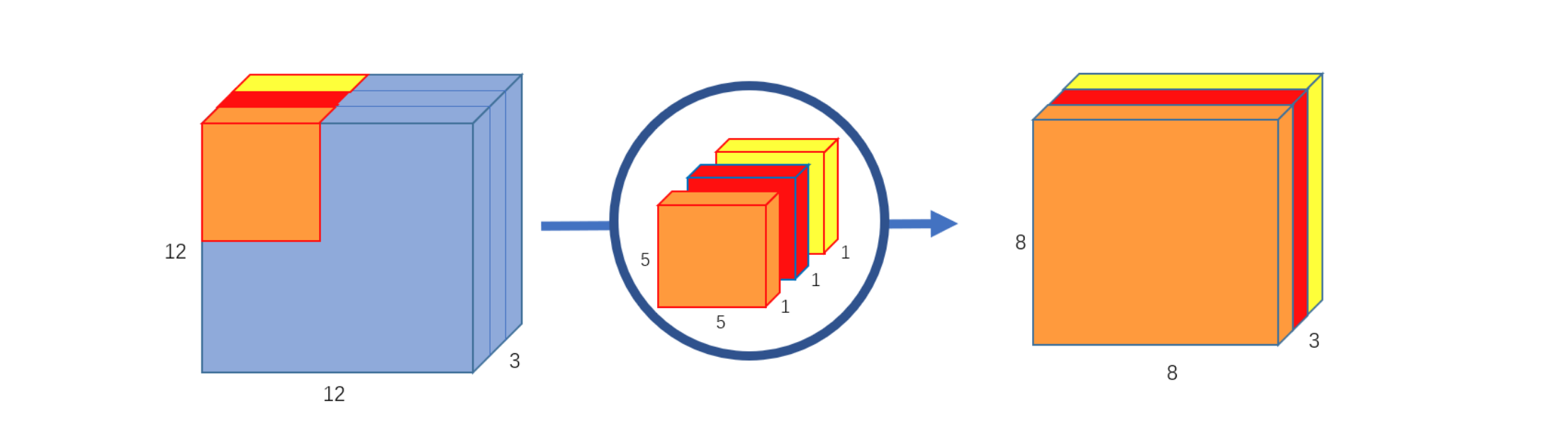
Figure 7. Depthwise convolution of a size 12 map (size = 5, stride = 1)

At the second stage, the point kernel is used to obtain the desired number of output maps (in the figure, the number of output maps is 256):

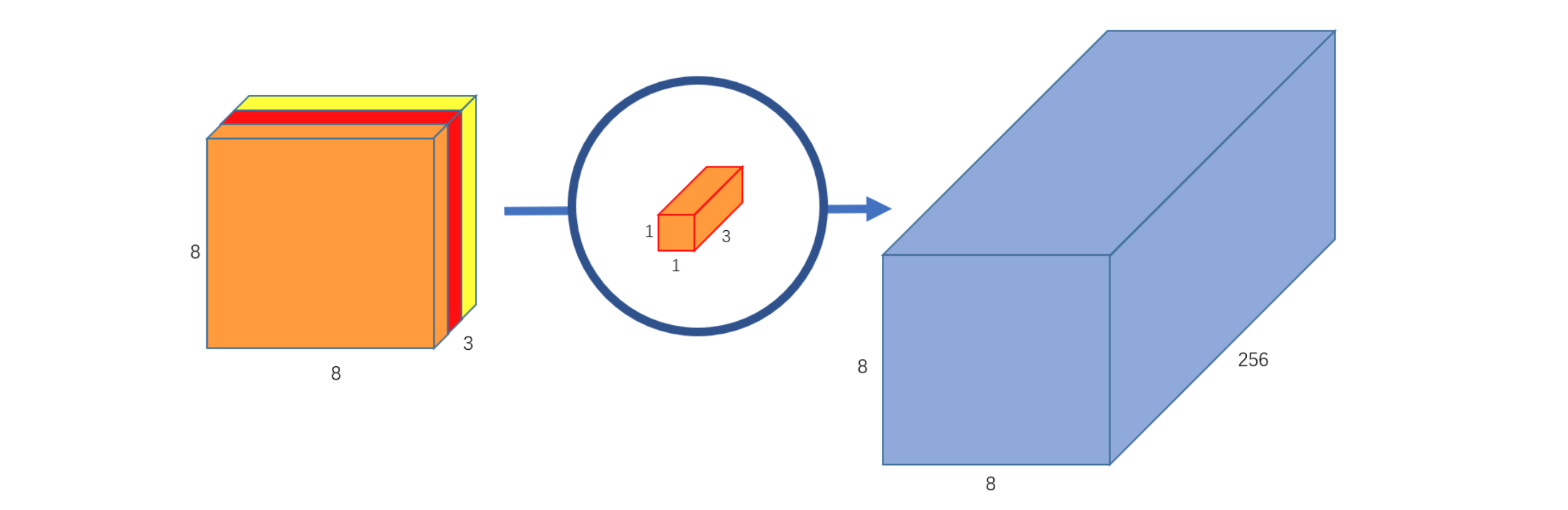
Figure 8. Pointwise convolution of a size 8 map (size = 1, stride = 1)

That is, we can say that one convolution layer with weights of shape $(C_{out}, C_{in}, size, size)$ was replaced with two convolutions: depthwise $(C, 1, size, size)$ and then pointwise $(C_{out}, C, 1, 1)$, where

$C_{out}$ - number of output tensor maps;
$C_{in}$ - number of input tensor maps;
$C$ - intermediate number of maps equal to $C_{in}$;
$size$ - kernel size.

Info

Within this library, depthwise convolution is performed by varying the groups parameter. See the derived classes examples for more details.

This technique can significantly reduce the amount of calculations.

Additional sources

• Detailed analysis of the padding technique: link;
• Article on dilated convolutions: link;
• Analysis of Depthwise convolution: link;

Initializing

def __init__(self, nd, inmaps, outmaps, size, stride=1, pad=0, dilation=1, wscale=1.0, useBias=True, name=None,
                 initscheme=None, empty=False, groups=1):

Parameters

Parameter	Allowed types	Description	Default
nd	int	Dimension of the operation	-
inmaps	int	Number of maps in the input tensor	-
outmaps	int	Number of maps in the output tensor	-
size	int	Convolution kernel size	-
stride	Union[int, tuple]	Convolution stride	1
pad	Union[int, tuple]	Map padding	0
dilation	Union[int, tuple]	Convolution window dilation	1
wscale	float	Random layer weights variance	1.0
useBias	bool	Whether to use the bias vector	True
initscheme	Union[tuple, str]	Specifies the layer weights initialization scheme (see createTensorWithScheme).	None -> ("xavier_uniform", "in")
name	str	Layer name	None
empty	bool	Whether to initialize the matrix of weights and biases	False
groups	int	Number of groups the maps are split into for separate processing	1

Explanations

See derived classes.