Skip to content

Activation

Описание

Info

Родительский класс: Module

Производные классы: -

Общая информация

Этот модуль реализует операцию активации слоя.

Функция активации - это заданная математическая операция над данными, которая добавляет нелинейность в преобразования нейронной сети.

Реализованные функции активации

Sigmoid

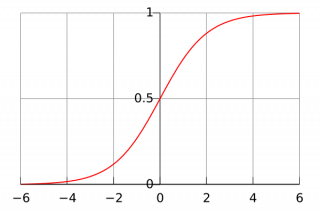
Принимает на вход произвольное вещественное число, а на выходе дает вещественное число в интервале от 0 до 1.

Вычисляется по формуле:

\begin{equation}\label{eq:sigmoid} σ(x) = \frac{1}{(1 + e^{-x})} \end{equation}

График функции:

сигмоида

Плюсы:

  • бесконечно дифференцируемая гладкая функция

Минусы:

  • насыщение сигмоиды приводит к затуханию градиента: в процессе обратного распространения ошибки локальный градиент, который может быть очень малым, умножается на общий - и в таком случае обнуляет его. Из-за этого сигнал почти не проходит через нейрон к его весам и рекурсивно к его данным;

  • выход сигмоиды не центрирован относительно нуля: нейроны в последующих слоях будут получать значения, которые также не центрированы относительно нуля, что оказывает влияние на динамику градиентного спуска.

Tanh

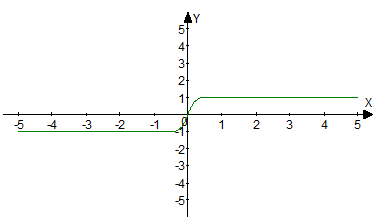
Принимает на вход произвольное вещественное число, а на выходе дает вещественное число в интервале от –1 до 1.

Вычисляется по формуле:

\begin{equation}\label{eq:hyptan} th(x) =\frac{e^x-e^{-x}}{e^x+e^{-x}} \end{equation}

График функции:

гиперболический тангенс

Плюсы:

  • бесконечно дифференцируемая гладкая функция
  • центрирована относительно нуля

Минусы:

  • проблема насыщения

ReLU

Реализует пороговый переход в нуле. Принимает значения на интервале [0, +∞). В данный момент ReLU является одной из самых популярных функций активации, а вокруг нее образовалось множество модификаций.

Вычисляется по формуле:

\begin{equation}\label{eq:relu} f(x) = \operatorname{max} (0, x) \end{equation}

Графики этой функции и двух ее нижеописанных модификаций:

все виды relu

Плюсы:

  • вычислительная простота
  • быстрота сходимости стохастического градиента

Минусы:

  • затухающий градиент (устраняется выбором соответствующей скорости обучения)
  • не гладкая функция

LeakyReLU

Модификация ReLU с добавлением малой константы α, при этом получаем, что при отрицательных значениях аргумента значение функции находится достаточно близко к нулю, но не равно ему. Принимает значения на интервале (-∞, +∞).

Вычисляется по формуле:

\begin{equation} \begin{matrix} \ f(x) & = & \left\{ \begin{matrix} \alpha x , & \mbox{если } x < 0 \\ x, & \mbox{если } x \geq 0 \end{matrix} \right. \end{matrix} \end{equation}

График приведен на изображении выше.

Плюсы:

  • вычислительная простота
  • быстрота сходимости стохастического градиента

Минусы:

  • затухающий градиент
  • не гладкая функция

ELU

Гладкая модификация ReLU и LeakyReLU. Принимает значения на интервале [-α, +∞).

Вычисляется по формуле:

\begin{equation} \begin{matrix} \ f(x) & = & \left\{ \begin{matrix} \alpha (e^x - 1), & \mbox{если } x < 0 \\ x, & \mbox{если } x \geq 0 \end{matrix} \right. \end{matrix} \end{equation}

График приведен выше.

Плюсы:

  • вычислительная простота
  • быстрота сходимости стохастического градиента
  • гладкая функция

Минусы:

  • затухающий градиент

SoftPlus

Гладкая функция активации. Принимает значения на интервале [0, +∞).

Вычисляется по формуле:

\begin{equation}\label{eq:softplus} f(x) = ln(1+e^x) \end{equation}

График функции:

софтплюс

Плюсы:

  • гладкая бесконечно дифференцируемая функция

Минусы:

  • не центрирована относительно нуля
  • затухающий градиент

Дополнительные источники

  • Статья на Википедии с большой сравнительной характеристической таблицей всех популярных функций активации.

Инициализация

def __init__(self, activation, slc=None, inplace=False, name=None, args=()):

Параметры

Параметр Возможные типы Описание По умолчанию
activation str Вид активации -
slc slice Срез, по которому будет вычислена функция активации None
inplace bool Если True, то выходной тензор будет записан в памяти на место входного False
name str Имя слоя None

Пояснения

activation - определяет выбранную функцию активации. Реализованные функции активации на данный момент: "sigmoid", "tanh", "relu", "leakyRelu", "elu", "softPlus", "clip".

inplace - флаг, показывающий, нужно ли выделять дополнительные ресурсы памяти для результата. Если True, то выходной тензор будет записан в памяти на место входного, что может негативно отразиться на работе сети, если входной тензор должен принимать участие в расчётах на других ветках графа.

Примеры

Необходимые импорты.

import numpy as np
from PuzzleLib.Backend import gpuarray
from PuzzleLib.Modules import Activation

Info

gpuarray необходим для правильного размещения тензора на GPU

Сформируем наглядные данные.

np.random.seed(123)
h, w = 3, 3
data = gpuarray.to_gpu(np.random.randint(-10, 10, (h, w)).astype(np.float32))
print(data)

[[  3.  -8.   -8.]
 [ -4.   7.    9.]
 [  0.  -9.  -10.]]

Допустим, нам интересен сигмоид в качестве функции активации. Инициализируем объект и отправим в него данные.

act = Activation('sigmoid')
print(act(data))

[[0.95257413  0.00033535017  0.00033535017]
 [0.01798621  0.999089       0.99987662  ]
 [0.5         0.00012339462  0.000045397865 ]]

ReLU:

act = Activation("relu")
print(act(data))

[[3. 0. 0.]
 [0. 7. 9.]
 [0. 0. 0.]]